ნიუტონის მეორე კანონი
გამოვარკვიოთ, თუ რომელი სიდიდით გამოისახება ძალა, ანუ, როგორც იტყვიან, რომელი სიდიდე გამოგვადგება სხეულზე მოქმედი ძალის ზომად. ამ კითხვაზე პასუხის გაცემა შეუძლია მხოლოდ ცდას. ცდა უნდა იყოს ასეთი: ერთი და იგივე ძალა უნდა მოვდოთ სხვადასხვა სხეულს და გავზომოთ ამ სხეულთა აჩქარებები. აჩქარებები ამ დროს შეიძლება იყოს სხვა და სხვა. მაგრამ ყველა ამ სხეულზე ერთი და იგივე ძალა თუ მოქმედებს, მაშინ უნდა ვიპოვოთ აჩქარებული სხეულების დამახასიათებელი ისეთი სიდიდე, რომელიც ყველა სხეულისათვის იქნება აგრეთვე ერთი და იგივე. სწორედ ეს სიდიდე გამოსახავს სხეულზე მოქმედ ძალას. ამჩქარებელ სხეულად, რომელიც ყველა სხეულზე ერთი და იმავე ძალით მოქმედებს, შეიძლება გამოდგეს გაჭიმული ან შეკუმშული ზამბარა. ეს იქედან ჩანს, რომ იგივე ზამბარა ნორმალურ მდგომარეობაში, ე. ი. როდესაც გაჭიმული (ან შეკუმშული) არ არის სრულებითაც არ მოქმედებს მასზე მიმაგრებულ სხეულზე რაიმე ძალით. მაშასადამე, დრეკადობის ძალა, რომლითაც ზამბარა მასზე მიმაგრებულ სხეულზე მოქმედებს, დამოვიდებულია მხოლოდ ზამბარის გაჭიმვაზე და არა მასზე მიმაგრებული სხეულის თვისებაზე. მაშ, გარკვეულ სიგრძეზე გაჭიმული (ან შეკუმშული) ზამბარა ყველა სხეულზე ერთი დაიმავე ძალით მოქმედებს. ზემოთ ნახსენები ცდა დაიყვანება იმაზე, რომ გარკვეულ სიგრძეზე გაჭიმულ ზამბარაზე მიმაგრებული სხვადასხვა სხეულის აჩქარებები გავზომოთ. როგორც 30-ე პარაგრაფში იყო აღნიშნული, უფრო მოხერხებულია გავზომოთ წრეწირზე მოძრავი სხეულების აჩქარება, ე. ი. ცენტრისკენული აჩქარება. ამიტომ კვლავ ვისარგებლებთ ცენტრიდანული მანქანით. ღერძული ნახვრეტის მქონე ცილინდრის ფორმის ალუმინის M სხეული მოვათავსოთ ცენტრიდანული მანქანის ღეროზე (ნახ. 86, ა). ცილინდრზე მივამაგროთ ზამბარის ერთი ბოლო, ხოლო მეორე დავამაგროთ მანქანის ჩარჩოზე A წერტილში.
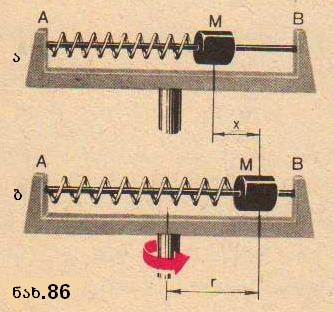
მანქანა ვაბრუნოთ. M ცილინდრი რამდენადმე დაშორდება ბრუნვის ღერძს (x მანძილით)და გაჭიმავს რა ზამბარას, იწყებს r რადიუსის მქონე წრეწირზე მოძრაობას(ნახ. 86, ბ). ცილინდრის ცენტრისკენული აჩქარება წრეწირის რადიუსის გასწვრივ ცენტრისკენ არის მიმართული. მაგრამ რადიუსის გასწვრივ არის მიმართული ზამბარის ღერძიც. მაშასადამე, M ცილინდრის აჩქარება ზამბარის ღერძის გასწვრივ არის მიმართული. ცხადია, რომ ცილინდრს ამ აჩქარებას ანიჭებს გაჭიმული ზამბარის დრეკადობის ძალა. ზამბარა რომ არ ყოფილიყო, ცილინდრი ხომ მოძვრებოდა ღეროს (მას რომ ხელს არ უშლიდეს საბრჯენი B წერტილში). როგორც ვიცით, ცენტრისკენული აჩქარების აბსოლუტური მნიშვნელობა, ტოლია
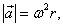
სადაც ω არის მანქანის ბრუნვის კუთხური სიჩქარე, ხოლო r იმ წრეწირის რადიუსია, რომელზედაც ცილინდრი მოძრაობს, ე.ი. მანძილი ცილინდრიდან ბრუნვის ღერძამდე. გავზომავთ რა ω კუთხურ სიჩქარეს და r რადიუსს, ვიპოვით 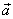 აჩქარების მოდულს. მანქანის ბრუნვის დროს ზამბარა მასზე მიმაგრებული სხეულით მით უფრო მეტად გაიჭიმება, რაც უფრო მეტი იქნება ბრუნვის კუთხური სიჩქარე. კუთხური სიჩქარის ყოველ მნიმვნელობას შეესაბამება გაჭიმული ზამბარის გარკვეული სიგრძე და, მაშასადამე, გარკვეული სიდიდის დრეკადობის ძალა. ახლა ალუმინის ცილინდრი (შევცვალოთ ზუსტად ასეთივე ზომის ფოლადის ცილინდრით. ვიცით, რომ მისი მასა ალუმინის ცილინდრის მასაზე სამჯერ მეტია. მანქანა კვლავ ბრუნვაში მოვიყვანოთ და შევარჩიოთ ამ ბრუნვის ისეთი სიჩქარე, რომ ზამბარის გაჭიმვა იყოს ისეთივე, როგორიც იყო ალუმინის ცილინდრის ბრუნვის დროს. მაშინ ფოლადის ცილინდრზე მოქმედი ძალაც ისეთივე იქნება. ცდა გვიჩვენებს, რომ ამ შემთხვევაში მანქანის ბრუნვის კუთხური სიჩქარე აჩქარების მოდულს. მანქანის ბრუნვის დროს ზამბარა მასზე მიმაგრებული სხეულით მით უფრო მეტად გაიჭიმება, რაც უფრო მეტი იქნება ბრუნვის კუთხური სიჩქარე. კუთხური სიჩქარის ყოველ მნიმვნელობას შეესაბამება გაჭიმული ზამბარის გარკვეული სიგრძე და, მაშასადამე, გარკვეული სიდიდის დრეკადობის ძალა. ახლა ალუმინის ცილინდრი (შევცვალოთ ზუსტად ასეთივე ზომის ფოლადის ცილინდრით. ვიცით, რომ მისი მასა ალუმინის ცილინდრის მასაზე სამჯერ მეტია. მანქანა კვლავ ბრუნვაში მოვიყვანოთ და შევარჩიოთ ამ ბრუნვის ისეთი სიჩქარე, რომ ზამბარის გაჭიმვა იყოს ისეთივე, როგორიც იყო ალუმინის ცილინდრის ბრუნვის დროს. მაშინ ფოლადის ცილინდრზე მოქმედი ძალაც ისეთივე იქნება. ცდა გვიჩვენებს, რომ ამ შემთხვევაში მანქანის ბრუნვის კუთხური სიჩქარე  –ჯერ ნაკლები იქნება. ეს ნიშნავს, რომ ფოლადის ცილინდრის აჩქარება 3-ჯერ ნაკლებია, ვიდრე ალუმინისა. აჩქარება აქაც მიმართულია ზამბარის ღერძის გასწვრივ (რადიუსის გასწვრივ წრეწირის ცენტრისაკენ). გამოდის, რომ თუ სხეულის მასას გავადიდებთ სამჯერ, იმავე სიდიდის ძალით გამოწვეული აჩქარება თავის მიმართულებას ინარჩუნებს, მაგრამ აბსოლუტური მნიშვნელობით 3–ჯერ შემცირდება. აქედან გამომდინარეობს, რომ სხეულის მასის ნამრავლი მის აჩქარებაზე ორივე შემთხვევაში ერთი და იგივეა. ასეთი ცდა შეიძლება ჩავატაროთ სხვადასხვა მასის მრავალ სხეულზე და ყოველი ცდა გვიჩვენებს, რომ ზამბარის ერთსა და იმავე სიგრმეზე გაჭიმვის შემთხვევაში, ე. ი. ერთი და იმავე ძალის დროს, სხეულის მასის ნამრავლი თავის აჩქარებაზე ყველა სხეულისათვის ერთი და იგივეა. ამგვარად, ვიპოვეთ სიდიდე, რომელიც სხვადასხვა სხეულისათვის ერთი და იგივეა, როდესაც მოქმედი ძალა ერთი და იგივეა, მაშასადამე, სხეულის მასის ნამრავლი თავის აჩქარებაზე გამოსახავს სხეულზე მოქმედ ძალას. თუ სხეულზე მოქმედ ძალას აღვნიმნავთ-F-ით, სხეულის აჩქარებას –ჯერ ნაკლები იქნება. ეს ნიშნავს, რომ ფოლადის ცილინდრის აჩქარება 3-ჯერ ნაკლებია, ვიდრე ალუმინისა. აჩქარება აქაც მიმართულია ზამბარის ღერძის გასწვრივ (რადიუსის გასწვრივ წრეწირის ცენტრისაკენ). გამოდის, რომ თუ სხეულის მასას გავადიდებთ სამჯერ, იმავე სიდიდის ძალით გამოწვეული აჩქარება თავის მიმართულებას ინარჩუნებს, მაგრამ აბსოლუტური მნიშვნელობით 3–ჯერ შემცირდება. აქედან გამომდინარეობს, რომ სხეულის მასის ნამრავლი მის აჩქარებაზე ორივე შემთხვევაში ერთი და იგივეა. ასეთი ცდა შეიძლება ჩავატაროთ სხვადასხვა მასის მრავალ სხეულზე და ყოველი ცდა გვიჩვენებს, რომ ზამბარის ერთსა და იმავე სიგრმეზე გაჭიმვის შემთხვევაში, ე. ი. ერთი და იმავე ძალის დროს, სხეულის მასის ნამრავლი თავის აჩქარებაზე ყველა სხეულისათვის ერთი და იგივეა. ამგვარად, ვიპოვეთ სიდიდე, რომელიც სხვადასხვა სხეულისათვის ერთი და იგივეა, როდესაც მოქმედი ძალა ერთი და იგივეა, მაშასადამე, სხეულის მასის ნამრავლი თავის აჩქარებაზე გამოსახავს სხეულზე მოქმედ ძალას. თუ სხეულზე მოქმედ ძალას აღვნიმნავთ-F-ით, სხეულის აჩქარებას 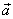 თი, ხოლო მასას m-ით მაშინ შეიძლება დავწეროთ: თი, ხოლო მასას m-ით მაშინ შეიძლება დავწეროთ:
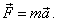
მაგრამ, შეიძლება ეს სწორი იყოს გაჭიმული ზამბარის დრეკადობის ძალისათვის და სხვა ძალებს არ ეხებოდეს? ამ კითხვას რომ ვუპასუხოთ, ჩავატაროთ კიდევ ერთი ცდა, რომელიც საშუალებას მოგვცემს სხვა ძალები შევადაროთ დრეკადობის ძალას. მაგალითად, სიმძიმის ძალა დრეკადობის ძალას შევადაროთ.
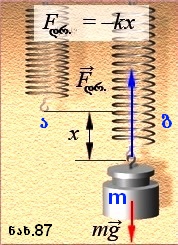
ამისათვის იგივე ზამბარა გამოვიყენოთ, მხოლოდ მისი ერთი ბოლო მივამაგროთ უძრავად და ვერტიკალურად მოვათავსოთ (ნახ.87, ა). ზამბარის ქვედა ბოლოზე ცნობილი m მასის ტვირთი ჩამოვკიდოთ (ნახ. 87, ბ). დავინახავთ., რომ ზამბარა გაიჭიმება, ხოლო ტვირთი უძრავი იქნება (რამდენიმე რხევის შემდეგ). ტვირთზე ახლა ერთდროულად ორი ძალა მოქმედებს: დედამიწის მხრიდან-სიმძიმის ძალა და გაჭიმული ზამბარის მხრიდან-დრეკადობის ძალა. რომ არ ყოფილიყო ზამბარა, ტვირთი დედამიწის გავლენით დაიწყებდა თავისუფალ ვარდნას ვერტიკალურად ქვევით მიმართული g=9,8 მ/წმ2 .აჩქარებით. მაგრამ, რადგან ტვირთის აჩქარება ნულის ტოლია, ეს ნიშნავს, რომ გაჭიმული ზამბარა თავის მხრივ ტვირთს ანიჭებს ვერტიკალურად ზევით მიმართულ აჩქარებას 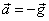 მაშასადამე, ტვირთზე მოქმედი F სიმძიმის ძალა და Fდრ დრეკადობის ძალა მაშასადამე, ტვირთზე მოქმედი F სიმძიმის ძალა და Fდრ დრეკადობის ძალა 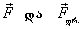 ,აბსოლუტური მნიმვნელობით ტოლია და მიმართულებით ერთი მეორის საწინააღმდეგო: ,აბსოლუტური მნიმვნელობით ტოლია და მიმართულებით ერთი მეორის საწინააღმდეგო: 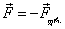 მაგრამ სხეულზე მოქმედი დრეკადობის ძალა, როგორც ეს ახლახან გამოვარკვიეთ, უდრის მასის ნამრავლს აჩქარებაზე, რომელსაც იგი სხეულს ანიჭებს, ე. ი. მაგრამ სხეულზე მოქმედი დრეკადობის ძალა, როგორც ეს ახლახან გამოვარკვიეთ, უდრის მასის ნამრავლს აჩქარებაზე, რომელსაც იგი სხეულს ანიჭებს, ე. ი.
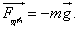
მაშასადამე, F სიმძიმის ძალა, რომელიც -Fდრ-ის ტოლია, იქნება:
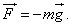
ამგვარად, დავადგინეთ, რომ სიმძიმის ძალაც უდრის სხეულის მასის ნამრავლს აჩქარებაზე რომელსაც ეს ძალა სხეულს ანიჭებს. ზემოთ განხილული ცდის მსგავსმა და კიდევ სხვა ცდებმა საშუალება მისცა ნიუტონს ჩამოეყალიბებია მექანიკის ერთ-ერთი უმნიშვნელოვანესი კანონი-ნიუტონის მეორე კანონი.
სხეულზე მოქმედი ძალა უდრის სხეულის მასისა და ამ ძალის მიერ მინიჭებულ აჩქარების ნამრავლს.
ნიუტონის მეორე კანონი მათემატიკურად გამოისახება ფორმულით
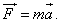
ნიუტონის მეორე კანონის გამომსახველი ფორმუმლიდან ჩანს თუ რა ერთეულებით იზომება ძალა.
ძალა ერთეულის ტოლია, თუ მისი მოქმედება ერთეული მასის სხეულს ერთეულის ტოლ აჩქარებას ანიჭებს.
SI სისტემაში ძალის ერთეულად მიღებულია ძალა, რომელიც 1 კგ მასას 1 მ/წმ 2 აჩქარებას ანიჭებს . ამ ერთეულს ეწოდება ნიუტონი (შემოკლებით: ნ)
1 ნ=1კგ.1მ/წმ2=1კგმ/წმ2.
CCS სისტემაში ძალის ერთეულად მიღებულია ძალა, რომელიც 1 გ მასას 1 სმ/წმ 2 აჩქარებას ანიჭებს. ამ ერთეულს ეწოდება დინი. (შემოკლებით დნ) .
1 დნ=1 გ.1 სმ/წმ2=1 გ.სმ/წმ2.
ნიუტონსა და დინს შორის თანაფარდობის მოძებნა ადვილია: 1ნ=1კგ.მ/წმ2=103 გ·102სმ/წმ2=105 გ·სმ/წმ2=105 დნ. მაგალითად, სიმძიმის ძალა, რომელიც 1 კგ მასის სხეულზე მოქმედებს, დედამიწის ზედაპირის მახლობლად: F=1 კგ.9,8 მ/წმ2=9,8 ნ=9,8.105 დნ. ნიუტონის მეორე კანონიდან გამოდის, და ამის გაგება მნიშვნელოვანია, რომ სხეულზე მოქმედი ძალები განსაზღვრავს მის აჩქარებას, ე. ი. სიჩქარის ცვლილებას და არა სხეულის მოძრაობის სიჩქარეს. ამიტომ აჩქარების მიმართულება მუდამ მოქმედი ძალის მიმართულების თანხვდენილია. ხოლო სიჩქარის მიმართულება, მაშასადამე, გადაადგილების მიმართულებაც, შესაძლებელია არ იყოს ძალის მიმართულების თანხვდენილი. ასე, მაგალითად, ძალა შეიძლება მუდამ მოძრაობის სიჩქარის პერპენდივულარული იყოს. ამ შემთხვევაში მოძრაობა წარმოებს წრეწირზე, ხოლო აჩქარება, ისე როგორც ძალა, მიმართულია იმ რადიუსის გასწვრივ, რომელიც გავლებულია მოძრავი სხეულიდან წრეწირის ცენტრისავენ. ასე მოძრაობდა სხეული დრეკადობის ძალის მოქმედებით ცენტრიდანულ მანქანაში. თუ სხეული ურთიერთქმედებაშია არა ერთ, არამედ რამდენიმე სხეულთან მაშინ მასზე მოქმედებს არა ერთი, არამედ რამდენიმე ძალა. ამასთანავე ძალები ერთიმეორეს ხელს ,,არ უშლის“ მიანიჭოს თავისი აჩქარება სხეულს, რომელზეც მოქმედებენ. ამიტომ, ერთობლივად მოქმედი ყველა
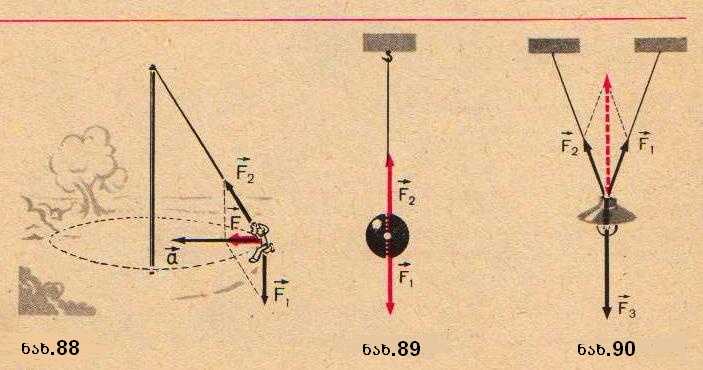
ძალის მიერ გამოწვეული სხეულიხ აჩქარება იქნება ისეთივე როგორსაც გამოიწვევდა ყველა ამ ძალoს ჯამის ტოლი ერთი ძალა. რადგანაც ძალა არის ვექტორული სიდიდე, ამიტომ ყველა ძალის ჯამში უნდა გვესმოდეს ვექტორული ჯამი. ასეთჯამს ეწოდება სხეულზე მოდებული ყველა ძალის ტოლქმედი. 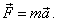 ფორმულაშიც, რომელიც ნიუტონის მეორე კანონს გამოსახავს, F წარმოადგენს სხეულზე მოქმედი ყველა ძალის ტოლქმედს. მოვიყვანოთ უბრალო მაგალითი. იმ საქანელაზე მოთავსებულ ადამიანზე, რომელსაც ,,გიგანტურ ნაბიჯებს“ უწოდებენ, ერთდროულად ორი ძალა მოქმედებს (ნახ. 88): დედამიწის მხრიდან ქვევით მიმართული F1 ძალა და ბაგირის მხრიდან F2 ძალა, რომელიც ბაგირის გასწვრივ არის მიმართული. ორი ძალის მოქმედების გამო ,,მგზავრი“ მოძრაობს წრეწირზე იმ ბოძის გარშემო, რომელზეც მიმაგრებულია ბაგირი. მაშასადამე, აჩქარება მიმართულია წრეწირის ცენტრისაკენ და არა F1 ან F2 ძალის გასწვრივ. ნახაზიდან ჩანს, რომ წრეწირის ცენტრისაკენ მიმართულია F ძალაც, რომელიც F 1 და F2 ძალების გეომეტრიული ჯამის ტოლია. მაშასადამე, „მგზავრი“ ისე მოძრაობს თითქოს მასზე მოქმედებდეს არა ორი ძალა: F1 და F2 არამედ მხოლოდ ერთი F ძალა - ამ ძალების ტოლქმედი: ფორმულაშიც, რომელიც ნიუტონის მეორე კანონს გამოსახავს, F წარმოადგენს სხეულზე მოქმედი ყველა ძალის ტოლქმედს. მოვიყვანოთ უბრალო მაგალითი. იმ საქანელაზე მოთავსებულ ადამიანზე, რომელსაც ,,გიგანტურ ნაბიჯებს“ უწოდებენ, ერთდროულად ორი ძალა მოქმედებს (ნახ. 88): დედამიწის მხრიდან ქვევით მიმართული F1 ძალა და ბაგირის მხრიდან F2 ძალა, რომელიც ბაგირის გასწვრივ არის მიმართული. ორი ძალის მოქმედების გამო ,,მგზავრი“ მოძრაობს წრეწირზე იმ ბოძის გარშემო, რომელზეც მიმაგრებულია ბაგირი. მაშასადამე, აჩქარება მიმართულია წრეწირის ცენტრისაკენ და არა F1 ან F2 ძალის გასწვრივ. ნახაზიდან ჩანს, რომ წრეწირის ცენტრისაკენ მიმართულია F ძალაც, რომელიც F 1 და F2 ძალების გეომეტრიული ჯამის ტოლია. მაშასადამე, „მგზავრი“ ისე მოძრაობს თითქოს მასზე მოქმედებდეს არა ორი ძალა: F1 და F2 არამედ მხოლოდ ერთი F ძალა - ამ ძალების ტოლქმედი: 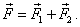 სხეულზე მოქმედი ძალების ვექტორული ჯამი შესაძლებელია ნულის ტოლიც იყოს. მაშინ სხეულის აჩქარებაც ნულის ტოლი იქნება, და სხეული იქნება უძრავი, ან წრფივად და თანაბრად.იმოძრავებს. ეს შემთხვევა გვქონდა მხედველობაში. როცა (ნიუტონის პირველი კანონი) ვლაპარაკობდით მოცემულ სხეულზე რამდენიმე სხეულის მოქმედებათა კომპენსირების შესახებ. ზონარზე ჩამოკიდებულ ბურთულას მაგალითში, რომელიც იქ განვიხილეთ, კომპენსირება იმაში მდგომარეობს, რომ ძალები, რომლითაც ბურთულაზე დედამიწა და ზონარი მოქმედებს, მიმართულებით ერთიმეორის საწინაადმდეგოა და აბსოლუტური მნიმვნელობებით ტოლი სხეულზე მოქმედი ძალების ვექტორული ჯამი შესაძლებელია ნულის ტოლიც იყოს. მაშინ სხეულის აჩქარებაც ნულის ტოლი იქნება, და სხეული იქნება უძრავი, ან წრფივად და თანაბრად.იმოძრავებს. ეს შემთხვევა გვქონდა მხედველობაში. როცა (ნიუტონის პირველი კანონი) ვლაპარაკობდით მოცემულ სხეულზე რამდენიმე სხეულის მოქმედებათა კომპენსირების შესახებ. ზონარზე ჩამოკიდებულ ბურთულას მაგალითში, რომელიც იქ განვიხილეთ, კომპენსირება იმაში მდგომარეობს, რომ ძალები, რომლითაც ბურთულაზე დედამიწა და ზონარი მოქმედებს, მიმართულებით ერთიმეორის საწინაადმდეგოა და აბსოლუტური მნიმვნელობებით ტოლი 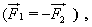 , რის გამოც მათი ტოლქმედი ნულის ტოლია (ნახ. 89). , რის გამოც მათი ტოლქმედი ნულის ტოლია (ნახ. 89).
90-ე ნახაზზე ნაჩვენებია შემთხვევა, როდესაც ნულს უდრის სხეულზე (ფარანზე) მოქმედი არა ორი, არამედ სამი ძალის 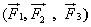 ტოლქმედი, ე. ი. ვექტორული ჯამი. თუ გამოვიყენებთ ძალის ცნებას. შეგვიძლია ახლა ნიუტონის პირველი კანონი სხვანაირად ჩამოვაყალიბოთ. ტოლქმედი, ე. ი. ვექტორული ჯამი. თუ გამოვიყენებთ ძალის ცნებას. შეგვიძლია ახლა ნიუტონის პირველი კანონი სხვანაირად ჩამოვაყალიბოთ.
არსებობს ათვლის სისტემები, რომელთა მიმართ სხეული წრფივად და თანაბრად მოძრაობს ან უძრავია, თუ სხეულზე მოქმედი ყველა ძალის ტოლქმედი ნულის ტოლია.
სინამდვილეში ეს დასკვნა სწორია მხოლოდ მატერიალური წერტილისათვის. ან სხეულისათვის, რომელიც მხოლოდ ვადატანითს მოძრაობას ასრულებს. სხეულზე მოქმედი ძალების ჯამი შეიძლება იყოს ნული. მაგრამ სხეული შეიძლება ბრუნავდეს. ამ დროს სხეულის წერტილები აჩქარებით მოძრაობენ.
შემდეგი გვერდი>>>
|







