კავშირი თანაბარაჩქარებულ მოძრაობასა და განვლილ მანძილს შორის
გადაადგილება თანაბარაჩქარებული მოძრაობისას, როდესაც მოძრაობის დრო უცნობია
ზოგჯერ საჭიროა თანაბარაჩქარებულად მოძრავი სხეულის გადაადგილების გამოთვლა, როდესაც ცნობილი არ არის მოძრაობის დრო, მაგრამ ცნობილია სხეულის საწყისი და საბოლოო სიჩქარეთა მნიშვნელობები. ამ შემთხვევაში გადაადგილების გამოსათვლელი ფორმულა შეიძლება მივიღოთ შემდეგნაირად: ჩვენთვის ცნობილია, რომ
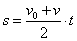 (1) (1)
ასევე აჩქარების გამოსათვლელი ფორმულიდან 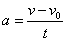 , გამოვითვალოთ: , გამოვითვალოთ: 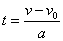 (2) თუ (1)–ში შევიტანთ t–ს მნიშვნელობას მივიღებთ: (2) თუ (1)–ში შევიტანთ t–ს მნიშვნელობას მივიღებთ: 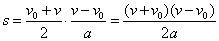
აქედან 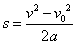 (3) (3)
ამგვარად მივიღეთ ფორმულა, რომლითაც შეიძლება გამოვთვალოთ გადაადგილება, თუ ცნობილია საწყისი და საბოლოო სიჩქარეები და აჩქარება.
ამ ფორმულით შეიძლება აგრეთვე ვიპოვოთ სხეულის 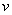 სიჩქარის მნიშვნელობები ნებისმიერ წერტილში, რომელზეც სხეული გაივლის. მოცემული განტოლებიდან(3): სიჩქარის მნიშვნელობები ნებისმიერ წერტილში, რომელზეც სხეული გაივლის. მოცემული განტოლებიდან(3):
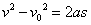 ან ან 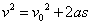 , ,
საიდანაც:
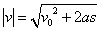 (4) თუ (4) თუ 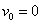 , მაშინ (3) დან , მაშინ (3) დან 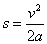 . . 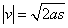
ამრიგად, წრფივი თანაბარცვლადი მოძრაობის განტოლებებია:
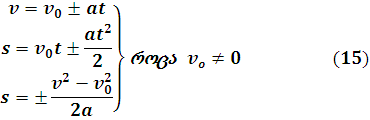
და
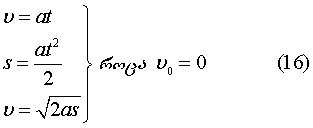
მე–15 ტოლობაში a აჩქარების აბსოლუტური სიდიდეა, უარყოფითი ნიშნის შეთხვევაში გვაქვს თანაბარშენელებული მოძრაობა. მე–16 ტოლობანი კი უსაწყისო სიჩქარით მოძრაობის შემთხვევაში თანაბარაჩქარებული მოძრაობის განტოლებებია, რადგან ამ დროს შენელებულ მოძრაობას აზრი არა აქვს და a>0 ყოველთვის. (15) და (16) განტოლებებს კინემატიკის განტოლებები ეწოდება.
| 






