სიჩქარე არათანაბარი მოძრაობისას. მყისი სიჩქარე
წრფივი თანაბარი მოძრაობა, რომლის დროსაც სხეული დროის ტოლ შუალედში ტოლ გადაადგილებას ასრულებს, ბუნებასა და პრაქტიკაში იშვიათია. უფრო ხშირად გვხვდება ისეთი მოძრაობები,როდესაც სხეული დროის ტოლ შუალედებში არათანაბარ მანძილს გადის. მოძრაობას, როდესაც სხეული დროის ტოლ შუალედებში არათანაბარ მანძილს გადის, არათანაბარი, ანუ ცვლადი მოძრაობა ეწოდება. ასე მოძრაობს დედამიწაზე და სივრცეში თითქმის ყველა სხეული: მატარებელი, ავტომობილი, გემი, ადამიანი, ცხოველი და სხვა სხვ. როცა ვამბობთ, მატარებელი ან ავტომობილი თანაბრად მოძრაობს, ვუშვებთ რაღაც მიახლოებას, რადგან მათი მოძრაობა თანაბარი არ არის. როდესაც მატარებელი სადგურს უახლოვდება, ადვილად შევამჩნევთ, რომ მისი მოძრაობა არათანაბარია.
უხეში გაზომვებითაც ადვილად დავრწმუნდებით, რომ მატარებელი ტოლი მანძილით დაშორებულ ტელეგრაფის ყოველ ორ ბოძს შორის მანძილის გავლას, სხვადასხვა დროს ანდომებს. როგორც ვხედავთ არათანაბარი მოძრაობის დროს იცვლება სხეულის სიჩქარე, ამიტომ ასეთ მოძრაობას ვერ დავახასიათებთ რაიმე გარკვეული სიჩქარით, მაგრამ თუ არ გვაინტერესებს მოძრაობა რომელიმე გარკვეულ უბანზე, მაშინ სხეულის მთელი მოძრაობის დასახასიათებლად შეიძლება შემოვიტანოთ საშუალო სიჩქარის ცნება. მართლაც, ვთქვათ, სხეული მოძრაობს არათანაბრად ისე, რომ პირველი წამის განმავლობაში ის გადაადგილდა 7 სმ–ით, მეორე წამის განმავლობაში – 10 სმ–ით, მესამე წამის განმავლობაში – 3 სმ–ით, მეოთხე წამის განმავლობაში – 4 სმ – ით, მაშინ ეს სხეული არათანაბარი მოძრაობით 4 წამში 24 სმ – ით გადაადგილდება. ამიტომ საშუალოდ იგი იმოძრავებს 24სმ/4წმ=6სმ/წმ სიჩქარით. მაშასადამე, არათანაბარი მოძრაობის საშუალო სიჩქარე იზომება სხეულის გადაადგილების მოდულის შეფარდებით იმ დროსთან, რა დროშიც მოხდა ეს გადაადგილება.
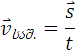
ასეთივე ფორმულა გვქონდა თანაბარი მოძრაობისათვის; მაშასადამე ცვლადი მოძრაობის საშუალო სიჩქარე ტოლია ისეთი თანაბარი მოძრაობის სიჩქარისა, რომლის დროსაც გადაადგილების მოდული და დრო ისეთივეა, როგორიც მოცემული ცვლადი მოძრაობისას. ამ განმარტების კარგად გასაგებათ განვიხილოთ ზემოთ მოყვანილი მაგალითო: საშუალო სიჩქარე პირველ წამში იქნებოდა
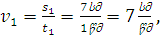 მეორეში – მეორეში –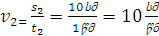 ,მესამეში – ,მესამეში – 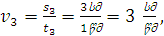 მეოთხეში – მეოთხეში –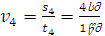 ; ჩვენ კი ვამბობთ, რომ ამ სხეულის საშუალო სიჩქარე მთელი დროის განმავლობაში იყო: ; ჩვენ კი ვამბობთ, რომ ამ სხეულის საშუალო სიჩქარე მთელი დროის განმავლობაში იყო:
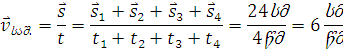
მაშინ როდესაც ასეთი საშუალო სიჩქარე სხეულს დროის არც ერთ შუალედში არ ჰქონია. ეს უნდა გავიგოთ ასე: სხეულს რომ თანაბრად ემოძრავა და 24 სმ გაევლო 4 წმ–ში, მაშინ მისი სიჩქარე იქნებოდა 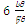 – –ის ტოლი. – –ის ტოლი.
საშუალო სიჩქარე შეიძლება განვიხილოთ, როგორც სკალარული სიდიდეც,
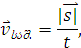
სადაც 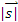 არის განვლილი მანძილი. ცხადია, საშუალო სიჩქარით ვერ განვსაზღვრავთ სხეული მდებარეობას დროის ნებისმიერ მომენტში. არის განვლილი მანძილი. ცხადია, საშუალო სიჩქარით ვერ განვსაზღვრავთ სხეული მდებარეობას დროის ნებისმიერ მომენტში.
მყისი სიჩქარე
თუ განვიხილავთ სხეულის ცვლადი მოძრაობის დროს გადაადგილებისა და დროის ძალიან მცირე მონაკვეთებს, მაშინ ამ გადაადგილებისა და დროის მცირე მონაკვეთში სხეულის მოძრაობა შეიძლება განვიხილოთ როგორც თანაბარი. ამიტომ ცვლადი მოძრაობა ტრაექტორიის რაიმე მცირე უბანზე და დროის მცირე მონაკვეთში შეიძლება დავახასიათოთ გარკვეული სიჩქარით, რომელსაც მყისი სიჩქარე ეწოდება. სხეულის სიჩქარეს დროის ნებისმიერ და ტრაექტორიის მოცემულ წერტილში მყისი ან ნამდვილი სიჩქარე ეწოდება. ვიცით, რომ წრფივი თანაბარი მოძრაობის სიჩქარე და წრფივი არათანაბარი მოძრაობის საშუალო სიჩქარე განისაზღვრება გადაადგილების ფარდობა იმ დროსთან, რომელიც დასჭირდა ამ გადაადგილებას. მყისი სიჩქარე კი განისაზღვრება, როგორც სიჩქარე დროის მოცემულ მომენტში და ტრაექტორიის მოცემულ წერტილში. გამოვარკვიოთ რას ნიშნავს სიჩქარე დროის მოცემულ მომენტში ან ტრაექტორიის მოცემულ წერტილში. ამისათვის განვიხილოთ რაიმე ზედაპირზე სხეულის წრფივი არათანაბარი მოძრაობა დაგამოვთვალოთ მისი მყისი სიჩქარე რომელიმე ო წერტილში (ნახ.1).
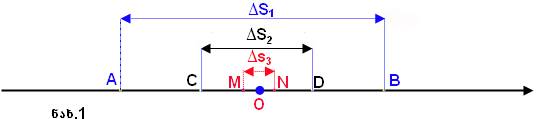
ამ მიზნით განვიხილოთ მცირე AB, CD და MN უბანი, რომელზეც შესაბამისად გადაადგილება ტოლი იყოს AB უბანზე 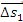 –ის, CD უბანზე –ის, CD უბანზე 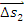 და MN უბანზე და MN უბანზე 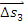 , ხოლო ამ გადადგილებებისათვის საჭირო დრო- , ხოლო ამ გადადგილებებისათვის საჭირო დრო- 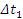 , , 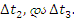 მაშინ საშუალო სიჩქარე AB უბანზე იქნება მაშინ საშუალო სიჩქარე AB უბანზე იქნება . უფრო მცირე CD უბნისათვის საუალო სიჩქარე იქნება . უფრო მცირე CD უბნისათვის საუალო სიჩქარე იქნება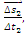 მაგრამ CD უბანზე სხეული უფრო ნაკლები სიდიდით მოასწრებს შეცვლას, ვიდრე AB უბანზე. კიდევ უფრო ნაკლებად შეიცვლება სხეულის მაგრამ CD უბანზე სხეული უფრო ნაკლები სიდიდით მოასწრებს შეცვლას, ვიდრე AB უბანზე. კიდევ უფრო ნაკლებად შეიცვლება სხეულის 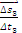 სიჩქარე უფრო მცირე MN უბანზე. თუ ასე გავაგრძელებთ უბნის სიგრძისა და იმ დროის შემცირებას, რომელიც ამ უბნის გავვლას სჭირდება, მაშინ ბოლოს უბანი იმდენად მცირე იქნება, რომ შეიძლება იგი იმ წერტილად მივიღოთ, რომელსაც უახლოვდება უბნები თანდათან შემცირების დროს (ნახ.1–ზე ეს იქნება O წერტილი), ხოლო შესაბამისი დრო – დროის „წერტილად" ანუ დროის მომენტად. სიჩქარე უფრო მცირე MN უბანზე. თუ ასე გავაგრძელებთ უბნის სიგრძისა და იმ დროის შემცირებას, რომელიც ამ უბნის გავვლას სჭირდება, მაშინ ბოლოს უბანი იმდენად მცირე იქნება, რომ შეიძლება იგი იმ წერტილად მივიღოთ, რომელსაც უახლოვდება უბნები თანდათან შემცირების დროს (ნახ.1–ზე ეს იქნება O წერტილი), ხოლო შესაბამისი დრო – დროის „წერტილად" ანუ დროის მომენტად.
სწორედ ამ მომენტში საშუალო სიჩქარე გახდება მყისი სიჩქარის ტოლი, რადგან ასე მცირე მონაკვეთზე სიჩქარის ცვლილება იმდენად უმნიშვნელო იქნება, რომ შეიძლება მისი უგულვებეყოფა, ე.ი. შეიძლება სიჩქარე მუდმივად ჩავთვალოთ, ამიტომ ამ მომენტისათვის არათანაბარ მოძრაობას განვიხილავთ, როგორც თანაბარ მოძრაობას.
მაშასადამე, მყისი სიჩქარე, ანუ სიჩქარე მოცემულ წერტილში, განისაზღვრება ამ წერტილის მახლობლობაში ტრაექტორიის მცირე უბანზე, საკმაოდ მცირე გადაადგილების შეფარდებით დროის იმ მცირე შუალედდთან, რომლის განმავლობაშიც მოხდა ეს გადაადგილება(უფრო ზუსტად იხილე აქ). მყისი სიჩქარე ვექტორული სიდიდეა, რომლის მიმართულება ემთხვევა მოცემულ წერტილში გადაადგილების მიმართულებას.
| 






