1.5 წრფივი თანაბარი მოძრაობასხვადასხვა
სხეულის მოძრაობას განასხვავებენ მათი დამახასიათებელი ნიშან–თვისებებით.
ტრაექტორიის ფორმის მიხედვით მოძრაობა შეიძლება იყოს წრფივი და მრუდწირული,
სიჩქარის მიხედვით – თანაბარი და არათანაბარი. წრფივი თანაბარი მოძრაობა
უმარტივესი მოძრაობაა. მოძრაობას, რომლის დროსაც სხეული დროის ნებისმიერ
ტოლ შუალედებში ტოლ გადაადგილებას ასრულებს, წრფივი თანაბარი მოძრაობა ეწოდება. ასეთ
მოძრაობას ასრულებს ავტომობილი წრფივ გზატკეცილზე, როდესაც უცვლელია მისი
ძრავას მუშაობა, პარაშუტისტი ვარდნისას, როდესაც გახსნილია პარაშუტი და
ა.შ. წრფივი თანაბარი მოძრაობა დროის ტოლ შუალედებში სხვადასხვა სხეულის
გადაადგილება სხვადასხვაა. მაგალითად, თუ ერთსა და იმავე დროის შუალედში
ავტომობილი მეტ გადაადგილებას ასრულებს, ვიდრე ველოსიპედი, მაშინ ამბობენ,
რომ ავტომობილი ველოსიპედზე სწრაფია. კოორდინატის ცვლილების სისწრაფის დამახასიათებელ ფიზიკურ სიდიდეს წარმოადგენს სიჩქარე. თუ წრფივი თანაბარი მოძრაობისას სხეულმა t დროის შუალედში შეასრულა 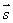 გადაადგილება, მაშინ სხეულის გადაადგილება, მაშინ სხეულის 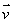 სიჩქარე გამოითვლება ფორმულით: სიჩქარე გამოითვლება ფორმულით: რადგან
წრფივი თანაბარი მოძრაობისას დროის ნებისმიერ ტოლ შუალედში სხეულის მიერ
შესრულებული გადაადგილებები ტოლია, ამიტომ სხეულის მოძრაობის სიჩქარე
მუდმივი სიდიდეა. ამგვარად, წრფივი თანაბარი მოძრაობის სიჩქარე არის
მუდმივი სიდიდე, რომელიც ტოლია ნებისმიერი დროის შუალედში სხეულის
გადაადგილების ფარდობისა ამ დროის შუალედთან. სიჩქარე ვექტორული სიდიდეა.
მისი მიმართულება ემთხვევა გადაადგილების ვექტორის მიმართულებას. თუ
ცნობილია სხეულის V სიჩქარე მაშინ t დროის შუალედში სხეულის გადაადგილება
რიცხვითი გამოსახულების ჩასატარებლად ვექტორული ტოლობების ნაცვლად უნდა
განვიხილოთ მათი გეგმილები კორდინატთა ღერძზე: საერთაშორისო ერთეულთა (SI) სისტემაში სიჩქარის ერთეულია 1მ/წმ. 1მ/წმ არის სიჩქარე, რომლის დროსაც წრფივად და თანაბრად მოძრავი ნივთიერი წერტილი 1წმ–ში 1მ–ით გადაადგილდება. არსებობს სიჩქარის სხვა ერთეულები: 1სმ/წმ, 1კმ/წმ და სხვა. დროის ნებისმიერ მომენტში სხეულის კოორდინატი გაომითვლება ფორმულით:
სადაც x სხეულის მდებარეობის კოორდინატია. ამ ფორმულაში ჩავსვათ გადაადგილების გეგმილის მნიშვნელობა, მივიღებთ:
ეს
ფორმულა წარმოადგენს კოორდინატის დროზე დამოკიდებულებას. იგი არის
მექანიკის ძირითადი ამოცანის ამოხსნა წრივი თანაბარი მოძრაობისთვის – მისი
საშუალებით შეიძლება განვსაზღვროთ წრფივად და თანაბრად მოძრავი სხეულის
მდებარეობა დროის ნებისმიერ მომენტში. სიჩქარის ვექტორის გეგმილი შეიძლება
იყოს დადებითიც და უარყოფითიც. თუ სხეულის სიჩქარის ვექტორი მიმართულია
კოორდინატთა ღერძის თანხვდენილად, მისი გეგმილი დადებითია, (სურ.1.17) თუ
ღერძის საპირისპიროდ – მაშინ გეგმილი უარყოფითია. (სურ.1.18) კოორდინატის
დროზე დამოკიდებულების ტოლობიდან შეიძლება განვსაზღვროთ სიჩქარის გეგმილი:
ამგვარად,
სიჩქარის გეგმილი კოორდინატთა ღერძზე ტოლია კოორდინატის ცვლილების
ფარდობისა იმ დროის შუალედთან, რომლის განმავლობაშიც ეს ცვლილება მოხდა.
| 






