სხეულთა
თავისუფალი ვარდნა. თავისუფლად ვარდნილი სხეულის აჩქარება
დედამიწა ყველა სხეულს იზიდავს
თავისი ცენტრისაკენ (მსოფლიო მიზიდულობა). ამიტომაა, რომ დედამიწის ზედაპირიდან რაღაც
სიმაღლეზე ატანილი სხეულები ვარდებიან დედამიწის ზედაპირზე. ძალას, რომლითაც დედამიწა
იზიდავს სხეულს, სიმძიმის ძალა ეწოდება. ამ ძალას დაწვრილებით ქვემოთ შევეხებით, ახლა
კი განვიხილოთ სხეულის ვარდნასთან დაკავშირებული კინემატიკის საკითხები. დაკვირვება
გვიჩვენებს, რომ დედამიწის ზედაპირიდან ერთი და იმევე სიმაღლეზე ატანილი სხეულებიდან
მძიმე სხეული უფრა ჩქარა ვარდება დედამიწის ზედაპირზე. IV საუკუნეში ჩვენს ერამდე ბერძენმა მეცნიერმა
არისტოტელემ გააკეთა დასკვნა, რომ ამის მიზეზი იყო სიმძიმის ძალის სხვადასხვაობა. ასეთი
აზრი არსებობდა თითქმის 20 საუკუნის მანძილძე. 1583 წელს იტალიელმა მეცნიერმა გალილეო
გალილეიმ(1564-1642) დაწვრილებით შეისწავლა სხეულების ვარდნა და დაასკვნა, რომ ჩვეულებრივ
პირობებში ვარდნილ სხეულებზე მოქმედებს არა მარტო სიმძიმის ძალა, არამედ ჰაერის წინაღობის
ძალაც. ცდებით გალილეიმ დაადგინა, რომ ჰაერის წინაღობის გარეშე ყველასხეული დედამიწის
ზედაპირის მოცემულ ადგილზე ერთნაირი აჩქარებით ვარდება წრფივად და თანაბარაჩქარებულად.
ჰაერის წინაღობა
ცვლის სხეულის ვარდნის კანონს, რადგან ჰაერის წინაღობის ძალა დამოკიდებულია სხეულის
ფორმასა და ზომაზე. ჰაერის წინაღობა ერთი და იმავე სიმაღლიდან ჩამოვარდნილი ფრინველის
ბუმბულის სიჩქარეს უფრო მეტად ამცირებს, ვიდრე ტყვიის მცირე ზომის საფანტისას. უჰაერო
სივრცეში კი ბუმბული და საფანტი ერთნაირი სიმაღლიდან ერთდროულად ჩამოვარდებოდნენ. ამას
მოწმობს მარტივი ცდები.
ავიღოთ
1მ სიგრძის მინის მილი, რომლის ერთი ბოლო დახშულია, მეორეზე კი აქვს ონკანი (სურ. 23). მასში მოთავსებულია სამი სხვადასხვა ფორმისა
და სიმძიმის სხეული: საფანტის მარცვალი, კორპის ბურთულა და ფრინველის ბუმბული. როცა
მილში ჰაერის წნევა ნორმალურია, ვერტიკალური მდებარეობიდან მილის 180°-ით სწრაფად გადმობრუნებისას,
პირველად ჩამოვარდება საფანტის მარცვალი, შემდეგ კორპი და ბოლოს ბუმბული (სურ. 23,ა)
ე.ი. ჰაერის წინაღობა სხვადასხვანაირად აფერხებს მათ მოძრაობას. თუ მილში ჰაერს საკმარისად
გავაიშვიათებთ და სწრაფად გადავაბრუნებთ, დავინახავთ, რომ სხეული ერთნაირი აჩქარებით
ვარდება.
უჰაერო სივრცეში
სხეულის ვარდნას სიმძიმის ძალის მოქმედებით, თავისუფალი ვარდნა ეწოდება.
სხეულის
თავისუფალი ვარდნის აჩქარებას აღნიშნავენ g ასოთი. 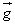 -ს სიმძიმის ძალის აჩქარებასაც უწოდებენ. -ს სიმძიმის ძალის აჩქარებასაც უწოდებენ. 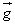 ვექტორი ყოველთვის მიმართულია ვერტიკალურად ქვემოთ. ვექტორი ყოველთვის მიმართულია ვერტიკალურად ქვემოთ. 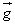 -ს სიდიდე და მიმართულება არ იცვლება თუ სხეული ჩამოვაგდეთ ზემოდან
ან ავისროლეთ -ს სიდიდე და მიმართულება არ იცვლება თუ სხეული ჩამოვაგდეთ ზემოდან
ან ავისროლეთ 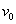 სიჩქარით. ამ შემთხვევაში სხეულის სიჩქარის ზრდა ან შემცირება g სიდიდით
დაიწყება სიჩქარით. ამ შემთხვევაში სხეულის სიჩქარის ზრდა ან შემცირება g სიდიდით
დაიწყება 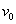 მნიშვნელობიდან. მნიშვნელობიდან.
თუ ვარდნისას X ღერძი მიმართულია ქვემოთ
სხეულის ვარდნის მიმართულებით, მაშინ 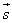 გადაადგილების, გადაადგილების,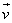 სიჩქარისა და სიჩქარისა და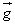 აჩქარების ვექტორების მიმართულებები ემთხვევა X ღერძის მიმართულებას,
მათი მოდულები აჩქარების ვექტორების მიმართულებები ემთხვევა X ღერძის მიმართულებას,
მათი მოდულები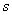 , ,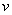 და g დადებითია
და ვექტორების გეგმილებია X ღერძზე. ვარდნილი
სხეულების გადაადგილებას აღნიშნავენ h-ით ან H
-ით. რადგან
სხეულის თავისუფალი ვარდნა
წრფივი
თანაბარაჩქარებული მოძრაობაა, ამიტომ მოძრაობის განტოლებები ასე გამოისახება: და g დადებითია
და ვექტორების გეგმილებია X ღერძზე. ვარდნილი
სხეულების გადაადგილებას აღნიშნავენ h-ით ან H
-ით. რადგან
სხეულის თავისუფალი ვარდნა
წრფივი
თანაბარაჩქარებული მოძრაობაა, ამიტომ მოძრაობის განტოლებები ასე გამოისახება:
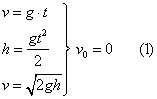
თუ დროის ათვლას დავიწყებთ ვარდნილი სხეულის მიერ რაიმე მანძილის გავლის
შემდეგ, ე.ი. როდესაც უკვე სხეულს აქვს რაღაც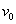 საწყისი სიჩქარე, მაშინ ვარდნილი სხეულის მოძრაობის განტოლებები
ასეთი იქნება: საწყისი სიჩქარე, მაშინ ვარდნილი სხეულის მოძრაობის განტოლებები
ასეთი იქნება:
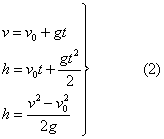
განვიხილოთ შემთხვევა, როცა სხეული 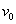 სიჩქარით მოძრაობას იწყებს
ვერტიკალურად ქვემოდან ზემოთ. X ღერძი მივმართოთ
ქვემოდან ზემოთ ვერტიკალურად, მაშინ სიჩქარით მოძრაობას იწყებს
ვერტიკალურად ქვემოდან ზემოთ. X ღერძი მივმართოთ
ქვემოდან ზემოთ ვერტიკალურად, მაშინ 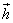 და და 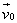 ვექტორების მიმართულება
ემთხვევა X ღერძის მიმართულებას და
მათი h და ვექტორების მიმართულება
ემთხვევა X ღერძის მიმართულებას და
მათი h და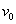 გეგმილები დადებითი სიდიდეებია. გეგმილები დადებითი სიდიდეებია. 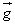 ვექტორის მიმართულება ამ დროს X ღერძზე უარყოფითია.
ცხადია, სხეულის მოძრაობა ამ დროს თანაბარშენელებულია და მოძრაობის განტოლებები ასეთ
სახეს ღებულობს: ვექტორის მიმართულება ამ დროს X ღერძზე უარყოფითია.
ცხადია, სხეულის მოძრაობა ამ დროს თანაბარშენელებულია და მოძრაობის განტოლებები ასეთ
სახეს ღებულობს:
 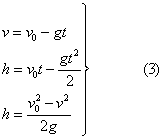
ტოლობები გამოსახავს ვერტიკალურად ზემოთ ასროლილი სხეულის მოძრაობის განტოლებებს.თუ
t1 ავღნიშნავთ
სხეულის მაქსიმალურ სიმაღლემდე ასვლის დროს, ამ სიმაღლეზე სხეულის სიჩქარე ნული ხდება,
ე.ი. საიდანაც საიდანაც

ასვლის მაქსიმალური სიმაღლის გამოსათვლელად  ფორმულაში უნდა დავუშვათ, რომ ფორმულაში უნდა დავუშვათ, რომ  ამიტომ გვექნება: ამიტომ გვექნება:

მაქსიმალური სიმაღლიდან სხეული იწყებს უსაწყისო სიჩქარით თავისუფალ ვარდნას
და დედამიწაზე ჩამოვარდება რაღაც t2 დროში, ამ დროს

საიდანაც

 ე.ი. ე.ი.

რა
დროსაც ანდომებს ვერტიკალურად ზევით ასროლილი სხეული მაქსიმალურ სიმაღლეზე ასვლას,
იმავე დროში ვარდება იგი უკან ამ სიმაღლიდან.
მაქსიმალური სიმაღლიდან ვარდნისას სხეულის საბოლოო სიჩქარე დედამიწაზე
დავარდნისას

ე.ი.

რა სიჩქარითაც ავისროლეთ
სხეული ვერტიკალურად ზემოთ იმ სიჩქარით დაბრუნდება იგი დედამიწაზე.
(4), (5), (6) და (7) დასკვნები მართებულია მხოლოდ უჰაერო სივრცეში მოძრაობისას,
რეალურად სხეულის ზემოთ მოძრაობისას ჰაერის წინაღობის ძალა და დედამიწის მიზიდულობის
ძალა სხეულის მოძრაობის საწინაარმდეგოდაა მიმართული. ეს ძალები მოდებულია სხეულზე.
ცხადია სხეულის სიჩქარე უფრო სწრაფად მცირდება, ვიდრე იდეალურ შემთხვევაში (ჰაერის
წინაღობის გათვალისწინების გარეშე) და სხეული  სიმაღლეზე ვერ ავა. სიმაღლეზე ვერ ავა.
ასვლის მაქსიმალური სიმაღლიდან სხეულის ვარდნისას ჰაერის წინაღობა ამცირებს
ვარდნილი სხეულის სიჩქარეს, რადგან ჰაერის წინაღობის ძალა მოძრაობის საპირისპიროდაა
მიმართული და იგი დედამიწაზე დაეცემა  -ზე ნაკლები სიჩქარით.
ქვემოთ ვნახავთ, რომ მოძრაობის სიჩქარის გადიდებასთან ერთად ჰაერის წინაღობის (ხახუნის) ძალები სიჩქარის პროპორციულად იზრდება,
ამოტომ დიდი სიჩქარით ასროლილი სხეულისთვის განსხვავება იდეალურ და რეალურ შემთხვევებს
შორის, მეტისმეტედ დიდია. მაგალითად, შაშხანიდან -ზე ნაკლები სიჩქარით.
ქვემოთ ვნახავთ, რომ მოძრაობის სიჩქარის გადიდებასთან ერთად ჰაერის წინაღობის (ხახუნის) ძალები სიჩქარის პროპორციულად იზრდება,
ამოტომ დიდი სიჩქარით ასროლილი სხეულისთვის განსხვავება იდეალურ და რეალურ შემთხვევებს
შორის, მეტისმეტედ დიდია. მაგალითად, შაშხანიდან  მ/წმ სიჩქარით ვერტიკალურად
ასროლილი ტყვია იდეალურ შემთხვევაში უნდა ავიდეს მ/წმ სიჩქარით ვერტიკალურად
ასროლილი ტყვია იდეალურ შემთხვევაში უნდა ავიდეს მ სიმაღლეზე.რეალურად
კი ტყვია ადის 2000-3000 მ სიმაღლეზე.
ასვლის მაქსიმალური სიმაღლიდან იგივე ტყვია უნდა ჩამოვარდნილიყო მ სიმაღლეზე.რეალურად
კი ტყვია ადის 2000-3000 მ სიმაღლეზე.
ასვლის მაქსიმალური სიმაღლიდან იგივე ტყვია უნდა ჩამოვარდნილიყო  მ/წმ სიჩქარით. რეალურ შემთხვევაში ტყვია ვარდება
50-60 მ/წმ სიჩქარით. როგორც ვხედავთ,
განსხვავება რეალურ და იდეალურ შემთხვევებს შორის მართლაც მეტისმეტად დიდია, რასაც
მეტად დიდი ყურადღება ეთმობა კოსმოსში რაკეტების და ჭურვების მოძრაობის ტრაექტორიის
დასადგენად და სხვ. მ/წმ სიჩქარით. რეალურ შემთხვევაში ტყვია ვარდება
50-60 მ/წმ სიჩქარით. როგორც ვხედავთ,
განსხვავება რეალურ და იდეალურ შემთხვევებს შორის მართლაც მეტისმეტად დიდია, რასაც
მეტად დიდი ყურადღება ეთმობა კოსმოსში რაკეტების და ჭურვების მოძრაობის ტრაექტორიის
დასადგენად და სხვ.
ჰაერის წინაღობის ძალის სიდიდე დამოკიდებულია სხეულის ფორმაზე. თუ სხეულს
კარგ გარსდენ ფორმას მივცემთ და ამავე დროს მისი ზომა მცირეა, მაშინ ჰაერის წინაღობას
მხედველობაში არ ღებულობენ.
ქვემოთ ვნახავთ, რომ დედამიწის მიერ სხეულის მიზიდვის ძალა დედამიწის ზედაპირიდან
დაშორების მიხედვით მცირდება, ამიტომ მცირდება g-ც. მაგრამ, თუ სხეულის ვარდნას
ვიხილავთ არა დიდი სიმაღლიდან, მაშინ g-ს ცვლილებას
უგულებელვყოფთ.
დედამიწის ზედაპირზე სიმძიმის ძალის აჩქარება იცვლება გეოგრაფიული განედის
მიხედვით. როგირც ვიცით განედი ეწოდება მერიდიანის გასწვრივ კუთხურ ამაღლებას ეკვატორის
სიბრტყიდან. ეკვატორზე განედი ნულია.პოლუსებზე ±90° . გაზომვები გვიჩვენებს, რომ  მ/წმ2, ხოლო მ/წმ2, ხოლო მ/მწმ2. 450განედზე g=9.81მ/წმ2 და მას
თვლიან ნრმალურ მნიშვნელობად. მიახლოებითი გამოთვლების დროს ზოგჯერ სიმძიმის ძალის
აჩქარებად ვღებულობთ g=9.8მ/წმ2 ან g=10მ/წმ2 თუ რატომ
იცვლება g განედის
მიხედვით ამას ქვემოთ გავარკვევთ. მ/მწმ2. 450განედზე g=9.81მ/წმ2 და მას
თვლიან ნრმალურ მნიშვნელობად. მიახლოებითი გამოთვლების დროს ზოგჯერ სიმძიმის ძალის
აჩქარებად ვღებულობთ g=9.8მ/წმ2 ან g=10მ/წმ2 თუ რატომ
იცვლება g განედის
მიხედვით ამას ქვემოთ გავარკვევთ.
| 






