სხეულის მასა
ინერტულობა, რომელიც ყოველ სხეულს გააჩნია, მისი ერთ.-ერთი უმნიმვნელოეანესი თვისებაა; მასზეა დამოკიდებული ის აჩქარება, რომელსაც სხეული მიიღებს სხვა სხეულებთან ურთიერთ ქმედების შედეგად.
სხეულთა ყოველგვარი თვისება გარკვეული სიდიდით გამოისახება მაგალითად, სხეულის ის თვისება, რომ მას სივრცის გარკვეული ნაწილი უჭირავს, სხეულის მოცულობის სიდიდით გამოისახება. სხეულთა თვისება, რომელსაც ინერტულობა ვუწოდეთ, გამოისახება აგრეთვე განსაკუთრებული სიდიდით. ასეთ სიდიდეს წარმოადგენს მასა. ურთიერთქმედი ორი სხეულიდან, რომელიც ნაკლებ აჩქარებას იღებს, ე. ი. მეტად ინერტულია, მას მეტი მასა აქვს. თუ ურთიერთ- ქმედი სხეულების მასებს აღვნიშნავთ m1 და m2, მაშინ შეიძლება დავწეროთ:
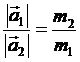
ურთიერთქმედი ორი სხეულის აჩქარებების აბსოლუტურ მნიშვნელობათა შეფარდება მათი მასების შებრუნებული შეფარდების ტოლია. მაგალითად, ჩვენ ვნახეთ, რომ ალუმინის ცილინდრის აჩქარების შეფარდება ფოლადის ცილინდრის აჩქარებასთან სამის ტოლია. ეს გამოწვეულია იმით, რომ ალუმინის ცილინდრის მასა სამჯერ ნაკლებია ფოლადის ცილინდრის მასაზე.
ამგვარად, ვიცით, როგორ მოიძებნება ორი სხეულის მასების შეფარდება. ამისათვის საჭიროა მათი აჩქარებების გაზომვა ურთიერთქმედების დროს. მაგრამ როგორ ვიპოვოთ ცალკე თითოეული სხეულის მასა? აქაც ისე უნდა მოვიქცეთ, როგორც სხვა სიდიდეების გაზომვის დროს. მაგალითად, რომ ვიპოვოთ, სხეულის მოცულობის გამომსახველი რიცხვი, ამისათვის ამ მოცულობას ვადარებთ რომელიღაც მოცულობას, რომელიც პირობით ერთეულად არის მიღებული, კუბურ მეტრს(მ3). ასეთივე ხერხით განსაზღვრავენ მასის რიცხვით მნიშვნელობას: რომ ვიპოვოთ ცალვე სხეულის მასის გამომსახველი რიცხვი, ამისათვის საჭიროა ავირჩიოთ რომელიმე სხეული, რომლის მასა პირობით ერთეულად იქნება მიღებული, – მასის ეტალონი. მემდეგ უნდა ჩავატაროთ ცდა, სადაც სხეული, რომლის მასასაც ვზომავთ, და მასის ეტალონი ურთიერთ ქმედებაშo მოვლენ (იხ. ნახ. 81). მაშინ ორივენი, სხეული და ეტალონი მიიღებს აჩქარებებს, რომლის გაზომვა შეიძლება, და დავწერთ ტოლობას
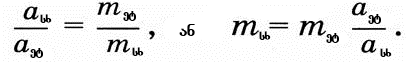
სადაც  სხეულის მასა და აჩქარებაა, ხოლო სხეულის მასა და აჩქარებაა, ხოლო 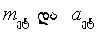 ეტალონის მასა და აჩქარება. მაგრამ ეტალონის მასა პირობით ერთეულის ტოლია, ამიტომ ეტალონის მასა და აჩქარება. მაგრამ ეტალონის მასა პირობით ერთეულის ტოლია, ამიტომ
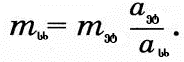
მასის ერთეულს.
სხეულის მასა არის სიდიდე, რომელიც მის ინერტულობას გამოსახავს. იგი განსაზღვრავს მასის ეტალონის აჩქარების შეფარდებას სხეულის აჩქარებასთან, უკანასკნელის ეტალონთან ურთიერთქმედების დროს. რომელ სხეულს მივიღებთ მასის ეტალონად, ეს სულერთია. საჭიროა მხოლოდ შეთანხმება, რომ ყველა ქვეყნისათვის იყოს ერთი და იგივე ეტალონი. 1889 წელს საერთაშორისო კონგრესზე მასის ეტალონად მიღებულ იქნა პლატინისა და ირიდიუმის შენადნობისაგან სპეციალურად დამზადებული ცილინდრის მასა. ამ ცილინდრის მასა არის სწორედ მასის საერთაშორისო ერთეული-კილოგრამი (შემოკლებით: კგ). მასის ეტალონი ინახება ზომისა და წონის საერთაშორისო ბიუროში (საფრანგეთმი). ყველა ქვეყანაში, არის ამ ეტალონის ზუსტი ასლი. დიდი სიზუსტით მეიძლება ჩავთვალოთ, რომ 1 ლ (1 დმ3) სუფთა წყალს 150C-ზე აქვს 1 კგ მასა. მასა ისეთ სიდიდეებთან ერთად, როგორიცაა სიგრძე და დრო, შედის ერთეულთა SI და CCS სისტემების ძირითად ერთეულთა რიცხვში. ერთეულთა CCS სისტემაში მასის ერთეულად მიღებულია გრამი (შემოკლებით: გ): 1გ=0,001 კგ. არ უნდა ვიფიქროთ, რომ ყოველთვის, როცა რაიმე სხეულის მასის გაზომვა არის საჭირო, ეს სხეული ურთიერთქმედებაში უნდა მოვიყვანოთ მასის ეტალონთან და შემდეგ გაიზომოს ამ სხეულისა და ეტალონის აჩქარებები. ასეთი ხერხი პრაქტივულად, რასაკვირველია, მოუხერხებელია. საბედნიეროდ არსებობს მასის გაზომვის სხვა ხერხი-აწონა, რომლითაც ჩვეულებრივ სარგებლობენ. მაგრამ ზოგ შემთხვევაში მასის განსაზღვრა ურთიერთქმედებით გამოწვეული აჩქარებებით ერთადერთი ხერხია. შეუძლებელია, მაგალითად, აწონით გაიზომოს პლანეტების, ვარსკვლავებისა და სხვა ციური სხეულების მასები. სასწორზე შეუძლებელია აგრეთვე ძალიან მცირე მასების გაზომვა, მაგალითად, ატომისა და მისი შემადგენელი ნაწილაკების მასების გაზომვა. სხეულის მასა მის საკუთარ თვისებას (ინერტულობას) გამოსახავს, რომელიც დამოვიდებული არ არის იმაზე, თუ რა სახის ურთიერთ- ქმედებაში მონაწილეობს სხეული, ან როგორ მოძრაობს. რაც არ უნდა ხდებოდეს სხეულზე, სადაც არ უნდა იმყოფებოდეს იგი და როგორც არ უნდა მოძრაობდეს, მისი მასა ერთი და იგივე რჩება. მასის ერთი საინტერესო და მნიშვნელოვანი თვისება შეიძლება გავიგოთ თუ ჩავატარებთ კიდევ ერთ ცდას (ნახ. 83)
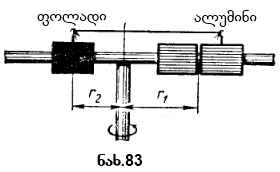 ალუმინის ორი ერთნაირი ცილინდრი შევაერთოდ და გავიმეოროთ ცდა ცენტრიდანულ მანქანაზე. ახლა ფოლადის ცილინდრი ურთიერთქმედებს არა ერთ, არამედ ორ ერთად შეერთებულ ალუმინის ცილინდრთან. ცდა გვიჩვენებს, რომ ორი ერთად შეერთებული ალუმინის ცილინდრის აჩქარების (შეფარდება ფოლადის ცილინდრის აჩქარებასთან ტოლია არა 3-ის, არამედ 3/2-ის. ეს ნიშნავს, რომ ერთად შეერთებული (თითქოს ერთ სხეულად ქცეული) ორი ცილინდრის მასა ორჯერ მეტია ერთ-ერთ მათგანზე. მაშასადამე, როდესაც ორ ან მეტ სხეულს ერთად ვაერთებთ, მათი მასები იკრიბება. მასის ამ თვისების საფუძველზე ზოგჯერ ამბობენ, რომ მასა გამოსახავს აგრეთვე ნიეთიერების რაოდენობას სხეულში. ხომ ცხადია, რომ ალუმინის ორ ცილინდრში ორჯერ მეტი ალუმინია, ვიდრე ერთში. ალუმინის ორი ერთნაირი ცილინდრი შევაერთოდ და გავიმეოროთ ცდა ცენტრიდანულ მანქანაზე. ახლა ფოლადის ცილინდრი ურთიერთქმედებს არა ერთ, არამედ ორ ერთად შეერთებულ ალუმინის ცილინდრთან. ცდა გვიჩვენებს, რომ ორი ერთად შეერთებული ალუმინის ცილინდრის აჩქარების (შეფარდება ფოლადის ცილინდრის აჩქარებასთან ტოლია არა 3-ის, არამედ 3/2-ის. ეს ნიშნავს, რომ ერთად შეერთებული (თითქოს ერთ სხეულად ქცეული) ორი ცილინდრის მასა ორჯერ მეტია ერთ-ერთ მათგანზე. მაშასადამე, როდესაც ორ ან მეტ სხეულს ერთად ვაერთებთ, მათი მასები იკრიბება. მასის ამ თვისების საფუძველზე ზოგჯერ ამბობენ, რომ მასა გამოსახავს აგრეთვე ნიეთიერების რაოდენობას სხეულში. ხომ ცხადია, რომ ალუმინის ორ ცილინდრში ორჯერ მეტი ალუმინია, ვიდრე ერთში.
ჩვენ ეამბობდით, რომ სხეულის მასა არ არის დამოკიდებული იმაზე, თუ როგორ მოძრაობს ეს სხეული. მაგრამ ეს მთლად სწორი არ. არის, ფარდობითობის თეორიას განსაცვიფრებელ დასკვნამდე მივყავართ, რომ სხეულის მასა მაინც დამოკიდებულია მის მოძრაობაზე. ადმოჩნდა, რომ სსეულის მასა სინამდვილეში მატულობს სიჩქარის ზრდასთან ერთად. დავუშვათ, რომ რომელიღაც უძრავი სხეულის მასა ტოლია m0-ის. თუ გაეზომავთ ამავე სხეულის. მასას, როდესაც იგი υ სიჩქარით მოძრაობს, ადმოჩნდება რომ მასა m0-ის ტოლი არ არის, არამედ
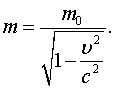
სადაც c-სინათლის სიჩქარეა. მაშასადამე, სხეულის მასა გადიდდა. მაგრამ მასის ეს გადიდება შესამჩნევია მხოლოდ ისეთი სიჩქარეების შეთხვევაში, რომლებიც ახლოა სინათლის სიჩქარესთან (c=3 .108 მ/წმ ). მასის გადიდებას შეუძლებელია ანგარიში არ გაეწიოს 260 000 კმ/წმ-ის და უფრო დიდი სიჩქარეებიხ დროს. მაგრამ ჩვეულებრივი სხეულები ასეთი სიჩქარით არასოდეს არ მოძრაობენ. ყველაზე სწრაფი სხეულები, რომლებთანაც საქმე შეიძლება გვქონდეხ, დედამიწის ხელოვნური თანამგზავრები და კოსმოსური ხომალდებია. მაგრამ მათი სიჩქარეები ჯერჯერობით 12 კმ/წმ არ აღემატება. ასეთი სიჩქარეების დროს კი შეიძლება ჩავთვალოთ, რომ მასა მუდმივია და სიჩქარეზე დამოკიდებული არ არის.
| 






