შ ე ს ა ვ ა ლ ი

წინა თავებში ვნახეთ, რომ თუ ცნობილია სხეულის აჩქარება და ვიცით აგრეთვე მისი საწყისი კოორდინატები და სიჩქარე, შეიძლება გამოვთვალოთ მისი სიჩქარე, გადაადგილება და ბოლოს, მისი კოორდინატიც დროის ნებისმიერ მომენტში. ახლა უნდა ვისწავლოთ სხეულის აჩქარების პოვნა. სხეულის მოძრაობა იწყება და წყდება, ხდება უფრო სწრაფი ან უფრო ნელი, იცვლება მოძრაობის მიმართულება. ყველა ამ შემთხვევაში საქმე გვაქვს სიჩქარის ცვლილებასთან, ე. ი. აჩქარების წარმოშობასთან. გასაგებია, თუ რამდენად მნიშვნელოვანია ვიცოდეთ რა პირობებში წარმოიშობა აჩქარება, რა პირობებში მოძრაობს სხეული აჩქარების გარეშე, როგორ განისაზღვრება აჩქარება (მისი აბსოლუტური სიდიდე და მიმართულება). ამის გარეშე არ შეიძლება მექანიკის ამოცანის გადაწყვეტა, ვერ შევძლებთ მოძრაობის მართვას. ყველა ამ კითხვაზე პასუხს იძლევა მექანიკის ძირითადი ნაწილი-დინამიკა.

მექანიკის ნაწილს, რომელშიც აჩქარების წარმოშობის მიზეზები შეისწავლება და მისი გამოთვლის ხერხები განიხილება, დინამიკა ეწოდება.

ნიუტონის პირველი კანონი

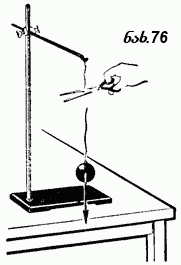
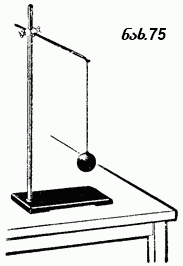აჩქარების წარმოშობის მიზეზი რომ ვიპოვოთ, ამისათვის ცდას, დაკვირვებას უნდა მივმართოთ. ჩვენთვის უფრო მოსახერხებელია ჯერ გამოვარკვიოთ, თუ რა პირობებში მოძრაობს სხეული აჩქარების გარეშე, ე. ი. რა პირობებში არ იცვლება სხეულის სიჩქარე დროის განმავლობაში. ყოველი სხეული, მომრავია თუ უძრავი, სამყაროში მარტოდ მარტო არ არის. მის გარშემო ბევრი სხვა სხეულია-მახლობელი და შორეული, დიდი და პატარა, უძრავი და მოძრავი. ბუნებრივია დავუშვათ, რომ ზოგი მათგანი და შეიძლება ყველაც, როგორღაც მოქმედებს სხეულზე, რომელსაც ვიხილავთ, როგორღაც გავლენას ახდენს მისი მოძრაობის მდგომარეობაზე. შეუძლებელია წინასწარ იმის თქმა, გარშემო მყოფი სხეულებიდან რომელი ახდენს არსებით გავლენას ამ მდგომარეობაზე და რომელი-უმნიშვნელოს. ეს უნდა გამოვიკვლიოთ ყოველ ცალკეულ შემთხვევაში.  ჯერ განვიხილოთ რომელიმე უძრავი სხეული. ასეთ სხეულს აჩქარება არ გააჩნია, მისი სიჩქარე მუდმივია და უდრის ნულს. 75-ე  ნახაზზე ნაჩვენებია რეზინის ზონარზე დაკიდებული ბურთულა. დედამიწის მიმართ იგი უძრავია. ბურთულას მახლობლად, მრავალი სხვადასხვა სხეულია: ზონარი, რაზედაც ის ჰკიდია; ოთახის კედლები; ამ ოთახში და მეზობელ შენობებში მოთავსებული საგნები და, რასაკვირველია, დედამიწაც. ცხადია, ყველა ეს სხეული ბურთულაზე ერთნაირად როდი მოქმედებს. მაგალითად, თუ ოთახში ავეჯს გადავდგამთ ან სულ გავიტანთ, ეს ბურთულაზე შესამჩნევ გავლენას არ მოახდენს. მაგრამ ზონარს თუ გადავჭრით (ნახ. 76), ბურთულა მაშინვე დაიწყებს ქვევით ვარდნას აჩქარებით. კარგად არის ცნობილი, რომ სახელდობრ დედამიწის გავლენით ყველა სხეული ვარდება ქვევით; მაგრამ ზონრის გადაჭრამდე ბურთულა მაინც უძრავ მდგომარეობამი იყო. ეს უბრალო ცდა გვიჩვენებს, რომ ბურთულას გარშემო მყოფი სხეულებიდან მასზე მესამჩნევ გავლენას მხოლოდ ორი ახდენს: რეზინის ზონარი და დედამიწა, და მათი ერთობლივი გავლენა განაპირობებს ბურთულას უძრაობის მდგომარეობას. საკმარისი აღმოჩნდა მოგვეხსნა ერთი მათგანი-ზონარი და უძრაობა დაირღვა. რომ შეგვძლებოდა ზონრის დატოვება და დედამიწის მოშორება, ესეც ბურთულას უძრაობის დარღვევას გამოიწვევდა: ბურთულა დაიწყებდა საწინააღმდეგო მიმართულებით მოძრაობას. აქედან შეიძლება დავასკვნათ, რომ ბურთულაზე ორი სხეულის ზონრისა და დედამიწის მოქმედება აკ ო მ პ ე ნ ს ი რ ე ბს (ზოგჯერ ამბობენ, ა წ ო ნ ა ს წ ო რ ე ბ ს) ერთმანეთს. როცა ამბობენ, რომ ორი 

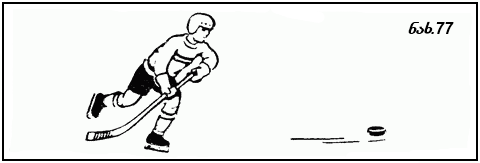
ან რამდენიმე სხეულის მოქმედება ერთმანეთს აკომპენსირებს, ეს ნიშნავს, რომ მათი ერთობლივი მოქმედების შედეგი ისეთივეა, როგორიც იქნებოდა ამ სხეულების გარეშე. განხილული მაგალითი და სხვა ბევრი მსგავსი მაგალითი საშუალებას იძლევა გავაკეთოთ შემდეგი დასკვნა: სხეულების მოქმედება თუ ერთმანეთს აკომპენსირებს, მაშინ ასეთი სხეულების გავლენით სხეული უძრავ მდგომარეობაშია. მაგრამ ვიცით, რომ მოძრაობა და უძრაობა ფარდობითია; და ათვლის ერთი სისტემის მიმართ თუ სხეული უძრავია, ათვლის სხვა სისტემის მიმართ შეიძლება მოძრაობდეს. მაგალითად, განვიხილოთ შაიბა, რომელიც ჰოკეის მოედნის ყინულზე ძევს (ნახ. 77). დედამიწის მიმართ შაიბა უძრავია, რადგანაც დედამიწის შაიბაზე მოქმედება კომპენსირდება ყინულის მოქმედებით. მაგრამ, დედამიწის მიმართ და, მაშასადამე, შაიბის მიმართ v სიჩქარით მოძრავი ჰოკეისტისათვის ეს შაიბა მოძრაობს ჰოკეისტის მოძრაობის საწინააღმდეგო მიმართულებით -v სიჩქარით. მოძრავ ჰოკეისტთან დაკავშირებულ ათგლის სისტემაში შაიბა მოძრაობს წრფივად და თანაბრად. შაიბას მოვარტყათ ჰოკიჯოხა. ამ ხანმოკლე მოქმედების შედეგად შაიბა. ამოძრავდება, მიიღებს რაღაც სიჩქარეს. აღსანიშნავია, რომ დარტყმის შემდეგ, როცა ჰოკიჯოხის მოქმედება შაიბაზე უკვე შეწყდა, შაიბა თავის მოძრაობას განაგრძობს. ამასთანავე, შაიბაზე სხვა სხეულების მოქმედება დარტყმის შემდეგ იგივე დარჩა, რაც დარტყმამდე იყო; წინანდებურად დედამიწის მოქმედება ყინულის მოქმე დებით კომპენსირდება, ხოლო ჰოკიჯოხა, ისე როგორც დარტყმამდე, არავითარ გავლენას არ ახდენს შაიბას მოძრაობაზე. შაიბა კი დარტყმის შემდეგ წრფივად და იმ მუდმივი სიჩქარით მოძრაობს, რომელიც მან დარტყმის მომენტში მიიღო. მართალია, ბოლოს და ბოლოს, შაიბა გაჩერდება, მაგრამ ცდით დასტურდება, რომ რაც უფრო გლუვია ყინული და თვით შაიბა, მით უფრო ხანგრძლივი იქნება შაიბას მოძრაობა. ამიტომ ადვილი მისახვედრია, რომ, თუ მთლიანად მოვხსნით ყინულის მოქმედებას შაიბაზე, ე. ი. მოვხსნით ხახუნს, მაშინ შაიბა დედამიწის მიმართ გაუჩერებლად იმოძრავებს მუდმივი სიჩქარით. ამრიგად, ვხედავთ, რომ, თუ 

სხეულზე სხვა სხეულების

მოქმედება კომპენსირდება, მაშინ დედამიწის მიმართ ეს სხეული ან უძრავია ან წრფივად  და თანაბრად მოძრაობს. მაგრამ ეს მტკიცება სამართლიანია არა ყველა ათვლის სისტემისათვის. მაგალითად, შეტევაზე გადასული ჰოკეისტისათვის, რომელიც დედამიწის მიმართ აჩქარებულად მოძრაობს, შაიბაც აგრეთვე არათანაბრად მოძრაობს. თუმცა, ეს ჰოკეისტიც, რასაკვირველია, იტყვის, რომ შაიბაზე დედამიწისა და ყინულის მოქმედება ერთმანეთს აკომპენსირებენ. ამგვარად, მივედით მექანიკის ერთ-ერთ ძირითად კანონამდე, რომელსაც ნიუტონის პირველი კანონი ეწოდება.

არსებობს ისეთი ათვლის სისტემები, რომელთა მიმართ მოძრავი სხეულები ინარჩუნებენ თავიანთ მუდმივ სიჩქარეს, თუ მათზე სხვა სხეულები არ მოქმედებს ან თუ სხვა სხეულების მოქმედება კომპენსირებულია.

თვით იმ მოვლენას, რომ გარეშე მოქმედებათა კომპენსირებისას სხეული ინარჩუნებს თავის მოძრაობის სიჩქარეს (კერძოდ, უძრაობის. მდგომარეობას), ინერციას უწოდებენ. ამიტომ, ნიუტონისხ პირველ კანონს, ხშირად ი ნ ე რ ც ი ი ს  კ ა ნ ო ნ ს უწოდებენ.

ათვლის სისტემებს, რომელთა მიმართ გარეშე მოქმედებათა კომპენსირებისას სხეული თანაბრად და წრფივად მოძრაობს, ეწოდება ათვლის ინერციული სისტემები.

ეს კანონი ეხება მატერიალურ წერტილს ან სხეულს, რომელიც გადატანითს მოძრაობაშია თუ სხეულზე სხვა სხეულების მოქმედებები ურთიერთკომპენსირდება, ამ სხეულს ბრუნვა მაინც შეუძლია, ბოლო ბრუნვის დროს სხეულის წერტილები აჩქარებით მოძრაობენ.

ზემოთ განხილულ ჰოკეის შაიბის მაგალითში ინერციულ სისტემას წარმოადგენს ათელის სისტემა, რომელიც დაკავშირებულია დედამიწასთან და ის სისტემაც, რომელიც დედამიწის მიმართ თანაბრად და წრფივად მოძრავ ჰოკეისტთან არის დაკაემირებული. მაგრამ არა მარტო ეს ორი. ცხადია, ათვლის ნებისმიერი სისტემა, რომელიც დედამიწის მიმართ წრფივად და თანაბრად მოძრაობს, ინერციულ სისტემას წარმოადგენს. ამგვარად, თუ ცდების საფუძველზე ცნობილი იქნება ათვლის თუნდაც ერთი ინერციული სისტემა, მაშინ ინერციული იქნება ნებისმიერი სხვა ათვლის სისტემა, რომელიც მის მიმართ წრფივად და ათანაბრად მოძრაობს. მემდეგში ვისარგებლებთ ათელის მხოლოდ ინერციული სისტემებით. ინერციის კანონი სრულიად ნათელი არ არის, როგორც ეს ერთი შეხედვით შეიძლება მოგვეჩვენოს. ამ კანონის აღმოჩენით  ბოლო მოეღო ერთ ძველთაგან მომდინარე შეცდომას. მანამდე, საუკუნეების მანძილზე მიაჩნდათ. რომ თუ ადგილი არა აქვს სხეულზე გარეშე მოქმედებას (ან,რაც იგივეა, როცა ყველა მოქმედებაკომპენსირებულია), იგი შეიძლება იყოს მხოლოდ უძრავ მდგომარეობაში, რომ უძრაობა სხეულის ბუნებრივი მდგომარეობაა. მუდმივი სიჩქარით სხეულის მოძრაობისათვის კი აუცილებელია მასზე სხვა სხეულის მოქმედება. თითქოს ამას ყოველდღიური გამოცდილება ამტკიცებდა: იმისათვის, რომ ოთხთვალა მუდმივი სიჩქარით მოძრაობდეს. მას ცხენი უნდა ეწეოდეს გამუდმებით; მაგიდამ იატაკზე რომ იმოძრაოს, საჭიროა მას განუწყვეტლიე ვეწეოდეთ ან ვაწვებოდეთ და ა. შ. დიდი იტალიელი მეცნიერი გალილეო გალილეი იყო პირველი, რომელმაც მიუთითა, რომ ეს სწორი არ არის, რომ გარედან მოქმედების გარეშე სხეულს შეუძლია იყოს არა მარტო უძრაც მდგომარეობაში, არამედ მოძრაობდეს წრფივად და თანაბრად. მაშასადამე, წრფივი და თანაბარი მოძრაობა წარმოადგენს სხეულების ისეთივე  ,,ბუნებრივ“ მდგომარეობას, როგორც უძრაობა. და თუ მაგიდის ასამოძრავებლად საჭიროა მას ვეწეოდეთ ან ვაწვებოდეთ, ეს იმით აიხსნება, რომ მაგიდის მომრაობის დროს იატაკი არა მარტო აკომპენსირებს დედამიწის მოქმედებას, არამედ წარმოშობს აგრეთვე მაგიდაზე დამატებით მოქმედებას, რომელსაც ხახუნი ეწოდება. იმათი მოქმედება, რომლებიც მაგიდას ეწევა ან აწვება, საჭიროა სწორედ ხახუნის კომპენსირებისათეის. გალილეიმ დაასკვნა, რომ თუ ადგილი არ ექნება ხახუნს, ერთხელ ამოძრავებული მაგიდა, შემდეგში მოქმედების გარეშე, მუდმივი სიჩქარით იმოძრავებს. გენიალურმა ინგლისელმა ფიზიკოსმა ისააკ ნიუტონმა გალილეის ეს დასკვნა განაზოგადა და მექანიკის ძირითადი კანონების რიცხვში შეიტანა.