80.  მსოფლიო მიზიდულობის ძალა

ნიუტონმა აღმოაჩინა სხეულთა მოძრაობის კანონები. ამ კანონების თანახმად აჩქარებული მოძრაობა შესაძლებელია მხოლოდ ძალის მოქმედებით  რადგან ვარდნილი სხეულები აჩქარებით მოძრაობენ, ამიტომ მათზე უნდა მოქმედებდეს ქვევით (დედამიწისაკენ) მიმართული ძალა. მაგრამ მხოლოდ დედამიწას გააჩნია მისი ზედაპირის მახლობლად მდებარე სხეულების მიზიდვის თვისება? 1667 წ. ნიუტონმა გამოთქვა მოსაზრება, რომ საზოგადოდ ყველა სხეულს შორის მოქმედებს ურთიერთმიზიდვის ძალები. მან ამ ძალებს მსოფლიო მიზიდულობიხ ძალები უწოდა. 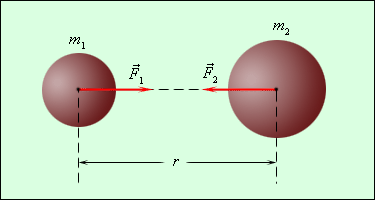მაშ, რატომ ვერ ვამჩნევთ ჩვენს გარემომცველ სხეულებს შორის ურთიერთმიზიდულობას? იქნებ ეს იმით აიხსნება, რომ მათ შორის მიზიდულობის ძალები მალიან მცირეა? ნიუტონმა შეძლო ეჩვენებინა, რომ სხეულებს შორის მიზიდულობის ძალის სიდიდე დამოკიდებულია ორივე სხეულის მასაზე და, როგორც გამოირკვა, საგრძნობ მნიშვნელობას მხოლოდ მაშინ აღწევს, როდესაც ურთიერთქმედი სხეულების (ან ერთ-ერთი მათგანის მაინც) მასა საკმაოდ დიდია.

ურთიერთმიმზიდველი სხეულების მასათა როლი. თავისუფალი ვარდნის აჩქარება საინტერესო თავისებურებებით გამოირჩევა ერთსა და იმავე ადგილზე იგი ერთნაირია ყველა სხეულისთვის, ნებისმიერი მასის სხეულისთვის. აჩქარება რომ არ არის მასაზე დამოკიდებული ამ უცნაური თვისების ერთადერთი ახსნა ის არის, რომ თვით F ძალა, რომლითაც დედამიწა სხეულს იზიდავს, სხეულის m მასის პროპორციულია. მართლაც, ამ შემთხვევაში სხეულის m მასის, ვთქვათ, ორჯერ გაზრდა გამოიწვევს F ძალის მოდულის ორჯერ გადიდებას, ხოლო აჩქარება, რომელიც F/m შეფარდების ტოლია, უცვლელი დარჩება. ნიუტონმაც სწორედ ეს ერთადერთი დასკვნა გააკეთა: მსოფლიო მიზიდულობის ძალა იმ სხეულის მასის პროპორციულია, რომელზეც იგი მოქმედებს. მაგრამ ვიცით, რომ სხეულები ურთიერთმიიზიდებიან და, ამასთანავე ურთიერთქმედება ყოველთვის ერთნაირი ბუნებისაა. მაშასადამე, ძალაც, რომლითაც სხეული დედამიწას იზიდავს, დედამიწის მასის პროპორციულია. ნიუტონის მესამე კანონის თანახმად, ეს ძალები მოდულებით ტოლია. მაშ, თუ ერთ-ერთი მათგანი დედამიწის მასის პროპორციულია, მაშინ მისი ტოლი მეორე ძალაც (რომლითაც დედამიწა სხეულს იზიდავს), აგრეთვე, დედამიწის მასის პროპორციულია. აქედან გამომდინარეობს, რომ ურთიერთმიზიდულობის ძალა ორივე ურთიერთქმედი სხეულის მასების პროპორციულია. ეს კი ნიშნავს, რომ ეს ძალა ორივე სხეულის მასების ნამრავლის ჰროპორციულია. კიდევ რაზეა დამოკიდებული ორი სხეულის მიზიდულობის ძალა?

სხეულთა შორის მანძილის როლი.  ნიუტონმა ივარაუდა, რომ ორ სხეულს შორის მიზიდულობის ძალა დამოკიდებული უნდა იყოს მათ შორის მანძილზე. ცდებით დადგენილია, რომ დედამიწის ზედაპირის მახლობლად თავისუფალი ვარდნის აჩქარება 9,8 მ/წმ²-ის ტოლია და იგი ერთნაირია სხეულებისთვის, რომლებიც ვარდებიან 1 მ, 10 მ და 100 მ სიმაღლიდან. მაგრამ ამის საფუძველზე ჯერ კიდევ ვერ დავასკვნით, რომ g აჩქარება არ არის დამოკიდებული დედამიწამდე მანძილზე.

ნიუტონს მიაჩნდა, რომ მანძილის ათვლა უნდა ხდებოდეს არა დედამიწის ზედაპირიდან, არამედ დედამიწის ცენტრიდან. დედამიწის რადიუსი კი 6400 კმ-ის ტოლია. ამიტომ გასაგებია, რომ დედამიწის ზედაპირიდან რამდენიმე ათეული ან ასეული მეტრი სიმაღლე შესამჩნევად ვერ შეცვლის თავისუფალი ვარდნის აჩქარებას. იმის გასარკვევად, თუ რა გავლენას ახდენს სხეულთა შორის მანძილი მათი ურთიერთმიზიდულობის ძალაზე, უნდა ვიცოდეთ რა აჩქარებით მოძრაობენ დედამიწის ზედაპირიდან დიდი მანძილით დაშორებული სხეულები.

ცხადია, დედამიწის ზედაპირიდან რამდენიმე ათასი კილომეტრის სიმაღლეზე მდებარე სხეულების თავისუფალი ვარდნის აჩქარების გაზომვა ძნელია. უფრო მოსახერხებელია სხეულის აჩქარების გაზომვა, როდესაც იგი თანაბრად მოძრაობს წრეწირზე დედამიწის გარშემო მისი მიზიდულობის ძალის ზემოქმედებით (ამ შემთხვევაში აჩქარება ცენტრისკენულია). გავიხსენოთ, რომ ასეთივე ხერხი გამოვიყენეთ დრეკადობის ძალის შესწავლის დროსაც, როდესაც ეზომავდით დრეკადობის ძალის მოქმედებით წრეწირზე მოძრავი ცილინდრის ცენტრისკენულ აჩქარებას.

მსოფლიო მიზიდულობის ძალის შესწავლაშ ფიზიკოსებს თვით ბუნება დაეხმარა და საშუალება მისცა მათ, განესაზღვრათ დედამიწის გარშემო წრეწირზე მომრავი სხეულის აჩქარება. ასეთი სხეულია დედამიწის ბუნებრივი თანამგზავრი - მთვარე. ნიუტონის ვარაუდი თუ სწორია, მაშინ უნდა ჩავთვალოთ, რომ დედამიწის გარიშემო წრეწირზე მოძრავ მთვარეს ცენტრისკენულ აჩქარებას ანიჭებს დედამიწის მიზიდულობის ძალა. დედამიწასა და მთვარეს შორის მიზიდულობის ძალა დამოკიდებული რომ არ ყოფილიყო მათ შორის მანძილზე, მთვარის ცენტრისკენული აჩქარება ისეთივე იქნებოდა, როგორიცაა სხეულთა თავისუფალი ვარდნის აჩქარება დედამიწის ზედაპირის მახლობლად.

სინამდვილეში კი, თავის ორბიტაზე მოძრავი მთვარის ცენტრისკენული აჩქარების სიდიდე, როგორც ვიცით,  0,0027 მ/წმ²-ის ტოლია. ეს სიდიდე დაახლოებით 3600-ჯერ ნაკლებია თავისუფალი ვარდნის აჩქარების სიდიდეზე დედამიწის ზედაპირის მახლობლად. ამავე დროს, ცნობილია მანძილი დედამიწისა და მთვარის ცენტრებს (შორის. იგი დაახლოებით 384 000 კმ-ის ტოლია და 60-ჯერ მეტია დედამიწის რადიუსზე, ე. ი. მანილზე დედამიწის ცენტრიდან მის ზედაპირამდე. ამრიგად, ურთიერთმიმზიდველ სხეულებს შორის მანძილის 60-ჯერ გადიდება იწვევს აჩქარების 60²-ჯერ შემცირებას. აქედან შეიძლება დავასკვნათ, რომ მსოფლიო მიზიდულობის ძალით გამოწვეული აჩქარება და, მაშასადამე, თვით ეს ძალაც ურთიერთქმედ სხეულთა შორის მანძილის კვადრატის უკუპროპორციულია. სწორედ ამ დასკვნამდე მივიდა ნიუტონი.

მსოფლიო მიზიდულობის კანონი. მაშასადამე, შეიძლება დავწეროთ, M და m მასის ორი სხეული ურთიერთმიიზიდება F ძალით, რომლის მოდულიც გამოისახება შემდეგი ფორმულით:

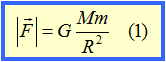
სადაც R  სხეულთა შორის მანძილია, ხოლო G -პროპორციულობის კოეფიციენტი, რომელიც ერთნაირია ბუნებაში არსებული ყველა სხეულისთვის. ამ კოეფიციენტს მსოფლიო მიზიდულობის მუდმივას ან გრავიტაციულ მუდმივას უწოდებენ. (1) ფორმულა გამოსახავს ნიუტონის მიერ აღმოჩენილ მსოფლიო მიზიდულობის კანონს.

ყველა სხეული ურთიერთმიიზიდება ძალით, რომლის მოდულიც პირდაპირ პროპორციულია მათი მასების ნამრავლისა და უკუპროპორციულია მათ შორის მანძილის კვადრატისა.

რა უნდა მივიჩნიოთ ურთიერთქმედ სხეულთა შორის მანძილად? გამოირკვა, რომ მსოფლიო მიზიდულობის კანონის გამომსახველი (1) ფორმულა მაშინ არის მართებული, როდესაც სხეულებს შორის მანძილი იმდენად დიდია მათს ზომებთან შედარებით, რომ შეიძლება ამ სხეულების ჩათვლა ნივთიერ წერტილად. ეს ძალა მიმართულია  ნივთიერი წერტილების შემაერთებელი წრფის გასწვრივ. ნივთიერ წერტილებად შეიძლება მივიჩნიოთ დედამიწა და მთვარე, პლანეტები და მზე მათ შორის მიზიდულობის ძალის გამოთვლისას. თუ სხეულებს სფეროს ფორმა აქვთ, ისინი ურთიერთმიიზიდებიან როგორც სფეროების ცენტრებში მოთავსებული ნივთიერი წერტილები იმ შემთხვევაშიც კი, როცა სხეულების ზომები მათ შორის მანძილის შესადარია.

ამ მემთხვევაში R სფეროთა ცენტრებს შორის მანძილია, ხოლო ძალა მიმართულია სფეროთა ცენტრების შემაერთებელი წრფის გასწვრივ. (1) ფორმულით შეიძლება აგრეთვე გამოითვალოს მიზიდულობის ძალა დიდი რადიუსის სფეროსა და მისი ზედაპირის ახლოს მდებარე ნებისმიერი ფორმის მცირე ზომის სხეულს შორის. ასეთ შემთხვევებში სხეულის, ზომები შეიძლება უგულვებელვყოთ  სფეროს რადიუსთან შედარებით. სწორედ ასე ვიქცევით დედამიწის სფეროსადმი სხვადასხვა სხეულის მიზიდულობის განხილვისას. ამ შემთხვევაში (1) ფორმულაში R დედამიწის სფეროს რადიუსია. მიზიდულობის ძალა კიდევ ერთი მაგალითია ისეთი ძალისა, რომელიც დამოკიდებულია ურთიერთქმედი სხეულების ურთიერთმდებარეობაზე, ე. ი. მათს კოორდინატებზე (ვინაიდან მიზიდულობის ძალა სხეულთა შორის მანძილზეა დამოკიდებული).

81. მსოფლიო მიზიდულობის მუდმივა

ნიუტონის მსოფლიო მიზიდულობის კანონის გამომსახველ ფორმულაში შედის G კოეფიციენტი მსოფლიო მიზიდულობის მუდმივა(გრავიტაციული მუდმივა). რა სიდიდეა იგი?

G კოეფიციენტს აქვს სრულიად გარკვეული და მარტივი აზრი. თუ ორივე ურთიერთქმედი სხეულის მასა ერთეულის ტოლია (M=m=1კგ)   და მათ შორის R  მანძილი აგრეთვე ერთეულის ტოლია (R=1 მ), მაშინ, როგორც ეს (1) ფორმულიდან ჩანს, F ძალა რიცხობრივად მსოფლიო მიზიდულობის მუდმივას (G) ტოლი იქნება.

 რა ერთეულებით გამოისახება G  მუდმივა? მსოფლიო მიზიდულობის კანონის გამომსახველი ფორმულიდან გამომდინარეობს, რომ

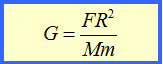
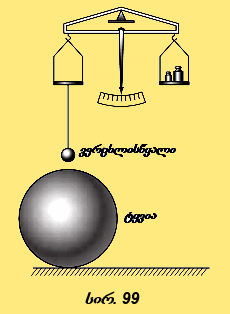თუ ძალა იზომება ნიუტონობით (ნ), მანძილი – (მ) მეტრობით   და, მასა-კილოგრამობით (კგ), მაშინ ტოლობის მარჯვენა ნაწილში მოთავსებული სიდიდე გამოისახება ნ·მ ²/კგ²-ით. ნებისმიერ ფორმულაში კი(თუ ეს ფორმულა   სწორია) ტოლობის ორივე მხარეს მოთავსებული სიდიდეები ერთი და იმავე ერთეულებით უნდა გამოისახოს (მაგალითად, 5 მ არ შეიძლება უდრიდეს 5კგ–ს). აქედან გამომდინარეობს, რომ SI  სისტემამი G მუდმივა უნდა გამოისახებოდეს ნ.მ ²/კგ ²-ით. რაც შეეხება მსოფლიო მიზიდულობის მუდმივას რიცხვით მნიშვნელობას, იგი შესაძლებელია განისაზღვროს მხოლოდ ცდით. ამ დროს, ცხადია, რაღაც ხერხით უნდა გაიზომოს F ძალა, რომელიც მოქმედებს ცნობილი r  მანძილით დაშორებული, ცნობილი m_l  და m₂ , მასების ორი სხეულიდან ერთ ერთზე. ასეთი ცდები არაერთგზის ჩატარდა. გავეცნოთ ერთ მათგანს: მგრძნობიარე სასწორის ერთ-ერთ პინაზე ჩამოკიდეს ვერცხლისწყლით სავსე მინის სფერო (სურ. 99), მეორეზე კი დააწყვეს საწონები, რომლებითაც გააწონასწორეს სასწორი. ზუსტი გაწონასწორების შემდეგ ვერცხლისწყლით სავსე სფეროს ქვეშ (მასთან რაც შეიძლება ახლოს) მოათავსეს დიდი მასის (დაახლოებით 6000 კგ) ტყვიის სფერო; რომელმაც მიიზიდა ვერცხლისწყლის სფერო. ამის გამო სასწორის წონასწორობა დაირღვა. მის აღსადგენად საჭირო გახდა საწონებიან პინაზე დამატებითი საწონის  მოთავსება. დამატებითი საწონის დედამიწისადმი მიზიდულობის ძალა, ცხადია, ტოლია ძალისა, რომლითაც ტყვიის სფერო იზიდავს ვერცხლისწყლის სფეროს, ე. ი.

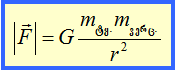
სადაც m_ტყ ტყვიის სფეროს მასაა, m_ვერ ვერცხლისწყლის სფეროს მასა, ხოლო r-მათ ცენტრებს შორის მანძილი. ამ ფორმულიდან ადვილად გამოითვლება G -ს მნიშვნელობა:

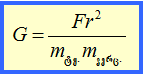
ამ ცდისა და კიდევ მრავალი ცდის საფუძველზე, მიღებულ იქნა გრავიტაციული მუდმივას მნიშვნელობა:

G = 6,67·10^–11 ნ ·მ ²/კგ ² (SI).

ეს ძალიან მცირე რიცხვია. სწორედ მისი სიმცირის გამოა, რომ ვერ ვამჩნევთ გარემომცველ სხეულებს შორის მიზიდულობას. ერთი მეტრი მანძილით დაშორებული თითო ტონა მასის ორი სფეროც კი ურთიერთმიიზიდება მხოლოდ ნიუტონის 6,67 მეასიათასედი ნაწილის ტოლი ძალით.