ჰორიზონტისადმი კუთხით გასროლილი სხეულის მოძრაობა
ვთქვათ სხეული გასროლილია 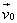 სიჩქარით, რომელიც ჰორიზონტთან ადგენს α კუთხეს (ნახ. 20ა). სიჩქარით, რომელიც ჰორიზონტთან ადგენს α კუთხეს (ნახ. 20ა).
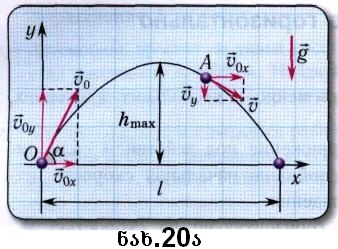 მივმართოთ კოორდინატთა სისტემის Ox ღერძი ჰორიზონტის გასწვრივ, მისი პერპენდიკულარული მიმართულებით კი-Oy ღერძი. ვიპოვოთ ამ ღერძზე მივმართოთ კოორდინატთა სისტემის Ox ღერძი ჰორიზონტის გასწვრივ, მისი პერპენდიკულარული მიმართულებით კი-Oy ღერძი. ვიპოვოთ ამ ღერძზე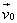 ვექტორის პროექციები: ვექტორის პროექციები:
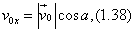
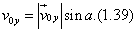
აღნიშნული პროექციები, როგორც ნახაზიდან ირკვევა, ამ შემთხვევაში დადებითია. კუთხით გასროლილი სხეულის მოძრაობა შეიძლება წარმოდგენილ იქნეს როგორც Ox და Oy ღერძის გასწვრივ ორი ერთმანეთისაგან დამოუკიდებელი მოძრაობის ჯამი. OY ღერძის მიმართულებით სხეული მოძრაობს  საწყისი სიჩქარით. ეს მოძრაობა არის თანაბრად შენელებული, ამიტომ საწყისი სიჩქარით. ეს მოძრაობა არის თანაბრად შენელებული, ამიტომ

თუ მხედველობაში მივიღებთ, რომ (1.40) და (1.41) ფორმულები გამოხატავენ  საწყისი სიჩქარით ვერტიკალურად ასროლილი სხეულის მოძრაობას, მაშინ α კუთხით გასროლილი სხეულისთვის დედამიწის ზედაპირიდან ასვლის მაქსიმალური სიმაღლე და შესაბამისი დრო გამოითვლება (1.34) და (1.33) ფორმულებით, თუ მასში საწყისი სიჩქარით ვერტიკალურად ასროლილი სხეულის მოძრაობას, მაშინ α კუთხით გასროლილი სხეულისთვის დედამიწის ზედაპირიდან ასვლის მაქსიმალური სიმაღლე და შესაბამისი დრო გამოითვლება (1.34) და (1.33) ფორმულებით, თუ მასში 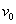 –ს შევცვლით –ს შევცვლით  –ის მნიშვნელობით (1.39)–დან. ამგვარად, –ის მნიშვნელობით (1.39)–დან. ამგვარად,
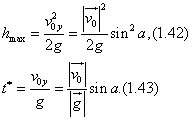
OX ღერძის მიმართულებით მოძრაობა წარმოებს 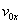 საწყისი სიჩქარით, რადგანაც დედამიწის მიზიდულობის ძალა OX ღერძის პერპენდიკულარულად არის მიმართული, ამიტომ მისი და შესაბამისად საწყისი სიჩქარით, რადგანაც დედამიწის მიზიდულობის ძალა OX ღერძის პერპენდიკულარულად არის მიმართული, ამიტომ მისი და შესაბამისად 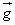 პროექცია OX ღერძზე ნულია. ამრიგად, OX ღერძზე გადაადგილების პროექციისათვის გვაქვს: პროექცია OX ღერძზე ნულია. ამრიგად, OX ღერძზე გადაადგილების პროექციისათვის გვაქვს:
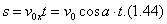
ჰორიზონტისადმი კუთხით გასროლილი სხეული სანამ დედამიწაზე დაეცემა, იგი  დროში მიაღწევს მაქსიმალურ დროში მიაღწევს მაქსიმალურ 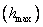 სიმაღლეს. შემდეგ იმავე დროში ვარდება დედამიწაზე. ამგვარად, OX ღერძის გასწვრივ სხეულის გადაადგილება ხდება სიმაღლეს. შემდეგ იმავე დროში ვარდება დედამიწაზე. ამგვარად, OX ღერძის გასწვრივ სხეულის გადაადგილება ხდება 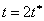 დროში თუ ამასთან გავითვალისწინებთ (1.43)-ს, მაშინ (1.44)-დან მივიღებთ ჰორიზონტისადმი კუთხით გასროლილი სხეულის დაშორებას გასროლის წერტილიდან დროში თუ ამასთან გავითვალისწინებთ (1.43)-ს, მაშინ (1.44)-დან მივიღებთ ჰორიზონტისადმი კუთხით გასროლილი სხეულის დაშორებას გასროლის წერტილიდან
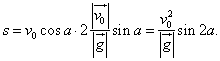
ამრიგად,
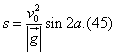
თუ (1.45) დავუშვებთ, რომ 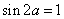 , ე.ი. , ე.ი. 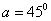 , მაშინ , მაშინ 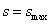 , ამგვარად, როდესაც ჰორიზონტისადმი კუთხით გასროლილი სხეულ;ის საწყისი სიჩქარის , ამგვარად, როდესაც ჰორიზონტისადმი კუთხით გასროლილი სხეულ;ის საწყისი სიჩქარის 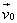 ვექტორი ჰორიზონტთან ადგენს ვექტორი ჰორიზონტთან ადგენს 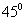 –ს , მაშინ სხეულის გადაადგილება OX ღერძის მიმასთულებით არის მაქსიმალური და –ს , მაშინ სხეულის გადაადგილება OX ღერძის მიმასთულებით არის მაქსიმალური და 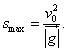 (1.46). თუ მხედველობაში მივიღებთ, (1.46). თუ მხედველობაში მივიღებთ,
რომ 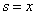 და და 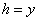 ,მაშინ (1.44) და (1.41) განტოლებიდან ,მაშინ (1.44) და (1.41) განტოლებიდან 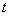 დროის გამორიცხვით ვღებულობთ დროის გამორიცხვით ვღებულობთ 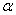 კუთხით გასროლილი სხეულის მოძრაობის ტრაექტორიის განტოლებას კუთხით გასროლილი სხეულის მოძრაობის ტრაექტორიის განტოლებას 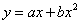 (1.47), სადაც (1.47), სადაც
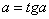 ; ; 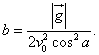 (1.47) წარმოადგენს იმ პარაბოლას განტოლებას, რომლის წვერო მდებარეობს (1.47) წარმოადგენს იმ პარაბოლას განტოლებას, რომლის წვერო მდებარეობს 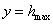 სიმაღლეზე. სიმაღლეზე.
| 






