გადაადგილება წრფივი თანაბარაჩქარებული მოძრაობის დროს.
ჩვენთვის ყველაზე მნიშვნელოვანია სხეულის გადაადგილების გამოთვლის ცოდნა. რადგან გადაადგილებით ვიპოვით სხეულის კოორდინატებს, ეს კი მექანიკის ძირითადი ამოცანაა. როგორ გამოვთვალოთ გადაადგილება თანაბარცვლადი მოძრაობის დროს? გადაადგილების განსაზღვრისათვის საჭირო ფორმულის მიღება ყველაზე უფრო მარტივად შეიძლება გრაფიკული მეთოდის გამოყენებით. ჩვენთვის ცნობილია, რომ წრფივი თანაბარი მოძრაობისას სხეულის გადაადგილება რიცხობრივად ტოლია სიჩქარის გრაფიკის ქვემოთ მოთავსებული ფიგურის(მართკუთხედის) ფართობისა. სამართლიანია თუ არა ეს თანაბარაჩქარებული მოძრაობისას? კოორდინატთა X ღერძის გასწვრივ სხეულის თანაბარაჩქარებული მოძრაობისას, სიჩქარე დროის განმავლობაში არ რჩება მუდმივი, იგი იცვლება დროის მიხედვით შემდეგი ფორმულების შესაბამისად:
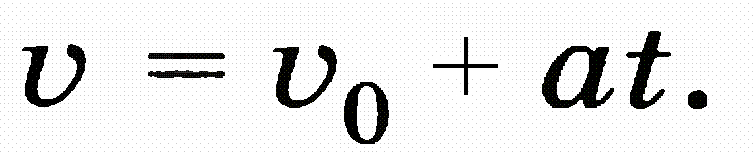 (1 ა) (1 ა)
ან
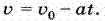 (1 ბ) (1 ბ)
ამიტომ სიჩქარის გრაფიკს აქვს ისეთი სახე, როგორიც ნაჩვენებია მე–39 ნახაზზე. ამ ნახაზზე მოცემული წრფე 1 შეესაბამება "დადებითი" აჩქარების მქონე მოძრაობას(სიჩქარე იზრდება), წრფე 2 კი – "უარყოფით" აჩქარების მქონე მოძრაობას(სიჩქარე კლებულობს) ორივე გრაფიკი ეხება შემთხვევას, როცა t=0 მომენტში სხეულს ჰქონდა v0 სიჩქარე. თანაბარაჩქარებული მოძრაობის სიჩქარის გრაფიკზე გამოვყოთ მცირე უბანი ab (ნახ.40).
.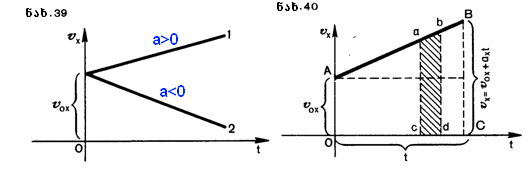
a დაb წერტილებიდან დავუშვათ პერპენდიკულარები t ღერძზე.cd მონაკვეთის სიგრძე t ღერძზე რიცხობრივათ ტოლი იქნება დროის იმ მცირე შუალედისა, რომლის დროსაც სიჩქარე შეიცვალა a წერტილის შესაბამის მნიშვნელობიდან b წერტილის შესაბამის მნიშვნელობამდე. გრაფიკის ab უბნის ქვემოთ მივიღეთ abdc ვიწრო ზოლი. რიცხობრივად cd მონაკვეთის ტოლი დროის შუალედი თუ საკმაოდ მცირეა, მაშინ სიჩქარის ცვლილება ამ დროის განმავლობაში აგრეთვე მცირე იქნება, ამ დროის შუალედში მოძრაობა შეიძლება ჩავთვალით თანაბრად, მაშინ abdc ზოლი მართკუთხედისაგან უმნიშვნელოდ განსხვავდება. ამიტომ abdcზოლის ფართობი რიცხობრივად ტოლი იქნება სხეულის გადაადგილებისა იმ დროის განმავლობაში, რომელიც cd მონაკვეთს შეესაბამება. მაგრამ ასეთ ვიწრო ზოლებად შეიძლება დავანაწილოთ სიჩქარის გრაფიკის ქვემოთ მოთავსებული მთელი ფიგურის ფართობი. მაშასადამე, მთელი t დროის შუალედში შესრულებული გადაადგილება რიცხობრივად OABC ტრაპეციის ფართობის ტოლი იქნება. ტრაპეციის ფართობი კი, ტოლია მისი ფუძეების ნახევარჯამის ნამრავლისა სიმაღლეზე. ჩვენ შემთხვევაში ტრაპეციის ერთ–ერთი ფუძე v0 –ს ტოლია, მეორე კი v –სი. სიმაღლე რიცხობრივად არის t–ს ტოლი. აქედან გამოდის, რომ s გადაადგილება უდრის: 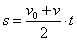 (2) ამ ფორმულაში v–ს ნაცვლად ჩავსვათ (1 ა) გამოსახულება, მაშინ (2) ამ ფორმულაში v–ს ნაცვლად ჩავსვათ (1 ა) გამოსახულება, მაშინ
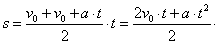
მრიცხველი წერ–წევრად გავყოთ მნიშვნელზე, მივიღებთ:
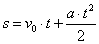 (2 ა) (2 ა)
(2)ფორმულაში v–ს ნაცვლად ჩავსვათ (1 ბ) გამოსახულება, მივიღებთ (იხ. ნახ.42):
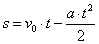 (2 ბ) (2 ბ)
(2 ა) ფორმულას იყენებენ იმ შემთხვევაში, როდესაც a აჩქარების ვექტორის მიმართულება ისეთივეა, როგორც კოორდინატთა ღერძის, ხოლო (2 ბ) ფორმულას მაშინ, როდესაც აჩქარების ვექტორის მიმართულება ამ ღერძის მიმართულების საწინააღმდეგოა. თუ v0=0 (ნახ. 43) და აჩქარების ვექტორის მიმართულება კოორდინატთა ღერძის მიმართულების თანხვდენილია, მაშინ (2 ა) ფორმულიდან გამოდის, რომ
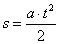
თუ აჩქარების ვექტორის მიმართულება კოორდინატთა ღერძის მიმართულების საწინააღმდეგოა, მაშინ (2 ბ) ფორმულიდან გამოდის, რომ
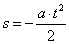
(აქ ნიშანი – გვიჩვენებს, რომ გადაადგილების ვექტორი, ისე როგორც აჩქარების ვექტორი, არჩეული ღერძის საწინააღმდეგოდ არის მიმართული). უნდა გვახსოვდეს, რომ (2 ა) და (2 ბ) ფორმულაში s და v0 სიდიდეები, რომლებიც 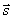 და და 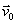 ვექტორების პროექციებს წარმოადენს, შეიძლება იყოს როგორც დადებითი, ისე უარყოფითიც. ახლა, როცა გადაადგილების გამოსათვლელი ფორმულები მიღებულია, ადვილად მივიღებთ სხეულის კოორდინატების გამოსათვლელ ფორმულებს. ჩვენთვის ცნობილია x კოორდინატის გამოსათვლელი ფორმულა: ვექტორების პროექციებს წარმოადენს, შეიძლება იყოს როგორც დადებითი, ისე უარყოფითიც. ახლა, როცა გადაადგილების გამოსათვლელი ფორმულები მიღებულია, ადვილად მივიღებთ სხეულის კოორდინატების გამოსათვლელ ფორმულებს. ჩვენთვის ცნობილია x კოორდინატის გამოსათვლელი ფორმულა: 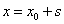 , ამიტომ თუ აჩქარების ვექტორს და კოორდინატთა ღერძს ერთნაირი მიმართულება აქვს, მაშინ , ამიტომ თუ აჩქარების ვექტორს და კოორდინატთა ღერძს ერთნაირი მიმართულება აქვს, მაშინ 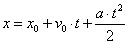 (3 ა) (3 ა)
და 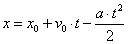 (3 ბ) (3 ბ)
თუ აჩქარების ვექტორს და კოორდინატთა ღერძს საწინააღმდეგო მიმართულება აქვს. სწორედ ეს არის ფორმულები, რომლების საშუალებას გვაძლევს ვიპოვოთ სხეულის მდებარეობა დროის ნებისმიერ მომენტში წრფივი თანაბარცვლადი მოძრაობის დროს.ამისათვის საჭიროა ვიცოდეთ სხეულის საწყისი კოორდინატი X0, მისი საწყისი სიჩქარე V0 და აჩქარება a.
| 






