გადაადგილება. ცნება ვექტორების შესახებ.

თუ ვიცით ნივთიერი წერტილის ტრაექტორია მისი საწყისი მდებარეობა, მაშინ საწყისი მდებარეობიდან ტრაექტორიის გასწვრივ გადავზომავთ ნივთიერი წერტილის მიერ განვლილ მანძილს და ვიპოვით მის მდებარეობას დროის მოცემულ მომენტში. მაგრამ ხშირად წინასწარ არ არის ცნობილი მოძრავი წერტილის მიმართულება და ტრაექტორია, მაგალითად ხომალდს, თვითმფრინავს, ადამიანს შეუძლია იმოძრაოს სხვადასხვა ტრაექტორიაზე, მაგრამ საწყისი მდებარეობისა და  დროში გავლილი გზის მიხედვით სხეულის მდებარეობას ყოველთვის ვერ დავადგენთ. მდებარეობის დასადგენად საჭიროა სიდიდე, რომელსაც გადაადგილება ეწოდება. რა სიდიდეა გადაადგილება?

ვთქვათ ნივთიერი წერტილი  დროის შემდეგ M მდებარეობას დაშორდა რაიმე  მანძილით. რომ ვიპოვთ ნივთიერი წერტილის ახალი K მდებარეობა, უნდა ვიცოდეთ, თუ რა მიმართულებით მოძრაობდა ნივთიერი წერტილი, ე.ი. ცნობილი უნდა იყოს იმ მონაკვეთის მიმართულება, რომელიც M მდებარეობას აერთებს K მდებარეობასთან. სხეულის საწყისი და მომდევნო მდებარეობების შემაერთებელი წრფის მიმართულ მონაკვეთს გადაადგილება ეწოდება (სურ. 3)

სიდიდეს, რომელიც ხასიათდება არა მარტო რიცხვითი მნიშვნელობით, არამედ მიმართულებითაც სივრცეში, ვექტორული სიდიდე ეწოდება. გადაადგილება ვექტორული სიდიდეა. ვექტორული სიდიდე გამოისახება წრფის ისრით დაბოლოებული მონკვეთით. მონაკვეთის სიგრძე არჩეული მასშტაბით გამოსახავს ვექტორის სიდიდეს, ხოლო ისარი გვიჩვენებს ვექტორის მიმართულებას. ვექტორული სიდიდის აღმნიშვნელ სიმბოლოს თავზე უკეთებენ ისარს. მაგალითად,  გადაადგილების ვექტორია (სურ. 3). ვექტორის რიცხვით მნიშვნელობას ვექტორის მოდული ეწოდება. ვექტორის მოდულს აღნიშნავენ ვერტიკალურ ხაზებში მოთავსებულ ისრიანი სიმბოლოთი ||, ან სიმბოლოთი ისრის გარეშე (S). ვექტორული სიდიდეებია: გადაადგილება, სიჩქარე, აჩქარება, ძალა, მოძრაობის რაოდენობა, ელექტრული ველის დაძაბულობა და სხვ.

სიდიდეს, რომელსაც არ გააჩნია სივრცეში მიმართულება და ხასიათდება მხოლოდ რიცხვითი მნიშვნელობით, სკალარული სიდიდე ეწოდება. სკალარული სიდიდეებია: გზა, ფართობი, მოცულობა, მასა მუშაობა, სიმძლავრე, ტემპერეტურა, სითბოს რაოდენობა, სითბოტევადობა, ელექტროტევადობა, პოტენციალი და სხვ.

ვექტორული სიდიდე კოორდინატთა ღერძებზე გამოისახება გეგმილებით (სურ. 4)

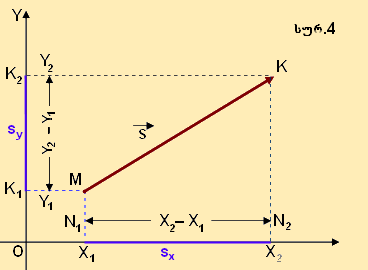
გადაადგილების  ვექტორის გეგმილებია OX და OY ღერძებზე (1)-დან  ვექტორის ბოლო წერტილის კოორდინატები იქნება

(2) ტოლობას მაშინ აქვს ადგილი, როცა ვექტორი  X და Y ღერძების მიმართულებასთან ქმნის მახვილ კუთხეებს. ერთნაირი მოდულისა და მიმართულების ორი ვექტორი ერთმანეთის ტოლია.