|
მოქმედებანი ვექტორებზე
1. ვექტორების შეკრება: ვთქვათ, ნივთიერი წერტილი სიბრტყეზე გადაადგილდება M1 მდებარეობიდან M2 მდებარეობაში. თუ ის გადაადგილდება M1M2 წრფის გასწვრივ, მაშინ  , თუ M1M2 წრფის გასწვრივ გადაადგილება შეუძლებელია, მაშინ ნივთიერი წერტილი ჯერ აღმოჩნდება სიბრტყის რომელიმე A მდებარეობაში M1A წრფის გავლით და შემდეგ A მდებარეობიდან A M2 წრფის გავლით M2 მდებარეობაში. საბოლოოდ შედეგი იგივეა. , თუ M1M2 წრფის გასწვრივ გადაადგილება შეუძლებელია, მაშინ ნივთიერი წერტილი ჯერ აღმოჩნდება სიბრტყის რომელიმე A მდებარეობაში M1A წრფის გავლით და შემდეგ A მდებარეობიდან A M2 წრფის გავლით M2 მდებარეობაში. საბოლოოდ შედეგი იგივეა.  და და  ორმა გადაადგილებამ შეცვალა ორმა გადაადგილებამ შეცვალა  გადაადგილება (სურ.5) შეგვიძლია დავწეროთ გადაადგილება (სურ.5) შეგვიძლია დავწეროთ  ან ან 

სადაც  და და  . ეს მაგალითი გვიჩვენებს . ეს მაგალითი გვიჩვენებს  და და  ვექტორების შეკრებას. ამ შეკრების დროს შესაკრები ვექტორები ისეა განლაგებული,რომ ვექტორების შეკრებას. ამ შეკრების დროს შესაკრები ვექტორები ისეა განლაგებული,რომ  ვექტორის ბოლო ემთხვევა ვექტორის ბოლო ემთხვევა  ვექტორის სათავეს,ხოლო ვექტორების ჯამი არის ვექტორის სათავეს,ხოლო ვექტორების ჯამი არის ვექტორი,რომელიც ვექტორი,რომელიც  ვექტორის სათავეს აერთებს ვექტორის სათავეს აერთებს  ვექტორის ბოლოსთან.ვექტორების შეკრების ეს წესი გამოიყენება რამდენიმე ერთგვაროვანი ვექტორის შეკრების დროს. ერთი და იმავე ფიზიკური სიდიდის შესაბამის ვექტორებს ერთგვაროვანი ვექტორები ეწოდება. ვექტორის ბოლოსთან.ვექტორების შეკრების ეს წესი გამოიყენება რამდენიმე ერთგვაროვანი ვექტორის შეკრების დროს. ერთი და იმავე ფიზიკური სიდიდის შესაბამის ვექტორებს ერთგვაროვანი ვექტორები ეწოდება.  ერთგვაროვანი ვექტორების შესაკრებად ერთგვაროვანი ვექტორების შესაკრებად  ვექტორის ბოლოს (სიდიდისა და მიმართულების შეუცვლელად) მივადოთ ვექტორის ბოლოს (სიდიდისა და მიმართულების შეუცვლელად) მივადოთ  ვექტორი.ანლოგიურად, ვექტორი.ანლოგიურად, ვექტორის ბოლოს მივადოთ ვექტორის ბოლოს მივადოთ  ვექტორი და ვექტორი და  ვექტორის ბოლოს მივადოთ ვექტორის ბოლოს მივადოთ  ვექტორი,ამის შემდეგ ვექტორი,ამის შემდეგ  ვექტორის სათავე წრფის მონაკვეთით შევუერთოთ ვექტორის სათავე წრფის მონაკვეთით შევუერთოთ  ვექტორის ბოლოს.მონაკვეთი მივმართოთ ისრით ვექტორის ბოლოს.მონაკვეთი მივმართოთ ისრით  ვექტორის დასაწყისიდან ვექტორის დასაწყისიდან  –ს ბოლოსაკენ.ეს იქნება მოცემული ვექტორების ვექტორული ჯამი(სურ.6,ა) –ს ბოლოსაკენ.ეს იქნება მოცემული ვექტორების ვექტორული ჯამი(სურ.6,ა)

მე–6 სურათზე ჩანს,რომ შესაკრები ვექტორების ადგილების შეცვლა ვექტორულ ჯამს არ ცვლის. ვექტორების შეკრების განხილულ წესს მრავალკუთხედის წესი ეწოდება.

განვიხილოთ ვექტორების შეკრების მეორე წესი. გადავიტანოთ  და და  ვექტორები (სიდიდისა და მიმართულების შეუცვლელად) სივრცის O ერტილში.შემდეგ ამ ვექტორებზე ავაგოთ პარალელოგრამი.O ერტილიდან გავლებული დიაგონალი გვაძლევს ვექტორები (სიდიდისა და მიმართულების შეუცვლელად) სივრცის O ერტილში.შემდეგ ამ ვექტორებზე ავაგოთ პარალელოგრამი.O ერტილიდან გავლებული დიაგონალი გვაძლევს  და და  ვექტორების ვექტორულ ჯამს (სურ.7) ვექტორების ვექტორულ ჯამს (სურ.7)


ვექტორების შეკრების ამ წესს პარალელოგრამის წესი ეწოდება.ვექტორების შეკრების ეს ორივე წესი ერთ შედეგს იძლევა,მაგრამ ბევრი ვექტორის შეკრებისას პარალელოგრამის წესის გამოყენება მოუხერხებელია.
|
ვექტორების შეკრების მრავალკუთხედის წესით იკრიბება ერთი წრფის გასწვრივ მიმართული(კოლინეალური) ექტორებიც. მე-8 სურათზე მოცემულია ერთსა და იმავე მხარეს მიმართული ვექტორების ჯამი. ხოლო მე-8 ა სურათზე -საპირისპიროდ მიმართული ვექტორების ჯამი, სურათიდან ჩანს, რომ კოლინეალური ვექტორები იკრიბება, როგორც ალგებრული სიდიდეები, ამისათვის ერთ-ერთ მიმართულებას მივაკუთვნებთ ,,+" ნიშანს, ხოლო მის საპირისპირო მიმართულებას - ,,-" ნიშანს.

კოორდინატთა ღერძზე რამდენიმე ვექტორის ვექტორული ჯამის გეგმილი შესაკრები ვექტორების გეგმილთა ალგებრული ჯამის ტოლია.
|


გეგმილი აითვლება დადებითად თუ შესაბამისი ვექტორი მოცემულ კოორდინატთა ღერძის მიმართულებასთან ადგენს მახვილ კუთხეს, ხოლო თუ ეს კუთხე ბლაგვია, მაშინ უარყოფითად, მე-9 სურათზე  ვექტორების გეგმილები X ღერძზე დადებითია, ხოლო ვექტორების გეგმილები X ღერძზე დადებითია, ხოლო  ვექტორის გეგმილი უარყოფითია. რომ ვიპოვოთ ვექტორების ჯამის გეგმილი არაა საჭირო ვექტორების ვექტორული ჯამის პოვნა და შემდეგ მისი გეგმილის განსაზღვრა, საკმარისია ვიპოვოთ შეკრებილი ვექტორების გეგმილები და შემდეგ მათი ალგებრული ჯამი. ამას დიდი გამოყენება აქვს ამოცანების ამოხსნის დროს. ვექტორის გეგმილი უარყოფითია. რომ ვიპოვოთ ვექტორების ჯამის გეგმილი არაა საჭირო ვექტორების ვექტორული ჯამის პოვნა და შემდეგ მისი გეგმილის განსაზღვრა, საკმარისია ვიპოვოთ შეკრებილი ვექტორების გეგმილები და შემდეგ მათი ალგებრული ჯამი. ამას დიდი გამოყენება აქვს ამოცანების ამოხსნის დროს.
ვექტორების შეკრების შებრუნებული ამოცანაა ვექტორების დაშლა ორ მდგენელ ვექტორად, ამისათვის საჭიროა იმ მდგენელი ვექტორების მიმართულებანი ( და და  სურ. 10), რომლებადაც უნდა სურ. 10), რომლებადაც უნდა 
დაიშალოს 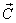 ვექტორი. ვექტორი. 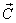 ვექტორის ბოლო წერტილიდან გავატაროთ ON და OM მიმართულებათა პარალელური წრფეები. მათ მიერ მოკვეთილი OK1 და OK2 მონაკვეთები მოგვცემს შემადგენელ ვექტორის ბოლო წერტილიდან გავატაროთ ON და OM მიმართულებათა პარალელური წრფეები. მათ მიერ მოკვეთილი OK1 და OK2 მონაკვეთები მოგვცემს შემადგენელ  და და  ვექტორების სიდიდეს. განვიხილოთ ასეთი ამოცანა. ვექტორების სიდიდეს. განვიხილოთ ასეთი ამოცანა.

მოცემულია 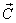 ვექტორი და მისი ერთ-ერთი ვექტორი და მისი ერთ-ერთი  მდგენელი ვექტორის სიდიდე და მიმართულება. ვიპოვოთ მდგენელი ვექტორის სიდიდე და მიმართულება. ვიპოვოთ 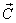 ვექტორის მეორე მდგენელი ვექტორის მეორე მდგენელი  ვექტორის სიდიდე და მიმართულება. ამისათვის ვექტორის სიდიდე და მიმართულება. ამისათვის 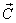 ვექტორის სათავეს (სიდიდესა და მიმართულების შეუცვლელად) მოვდოთ ვექტორის სათავეს (სიდიდესა და მიმართულების შეუცვლელად) მოვდოთ  ვექტორი (სურ. 11) ამის შემდეგ ვექტორი (სურ. 11) ამის შემდეგ  ვექტორის ბოლო შევუერთოთ ვექტორის ბოლო შევუერთოთ 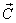 ვექტორის ბოლოს მიმართული მონაკვეთით მივიღებთ საძიებელ ვექტორის ბოლოს მიმართული მონაკვეთით მივიღებთ საძიებელ  ვექტორს. ვექტორს.
ორი ვექტორის ვექტორული ჯამის მოდული კოსინუსების თეორემის თანახმად (სურ. 7) ასე გამოისახება:

თუ  და (8) ტოლობა მოგვცემს: და (8) ტოლობა მოგვცემს:

 და (8) ტოლობიდან და (8) ტოლობიდან

 და (8) ტოლობიდან და (8) ტოლობიდან


მართკუთხა კოორდინატთა სისტემის ღერძებზე ვექტორის პროექციის საშუალებით ადვილად ვპოულობთ ვექტორის სიდიდესა და მიმართულებას (სურ. 12). სურათიდან ჩანს, რომ

ვექტორის მიმართულებას ვიპოვით შემდეგი ტოლობიდან:

2. ვექტორების სხვაობა:  და და  ვექტორების ასე გამოისახება: ვექტორების ასე გამოისახება:

( ) ვექტორი მოდულით ) ვექტორი მოდულით  ვექტორის ტოლია და მის საპირისპიროდაა ვექტორის ტოლია და მის საპირისპიროდაა

მიმართული. ამიტომ საჭიროა შეიკრიბოს  და ( და ( )ვექტორი ჩვენ მიერ ზემოთ განხილული წესით ( სურ. 13) მივიღებთ )ვექტორი ჩვენ მიერ ზემოთ განხილული წესით ( სურ. 13) მივიღებთ  და და  ვექტორების სხვაობას. ვექტორების სხვაობის პროექცია მოცემულ ღერძზე ტოლია ამავე ღერძზე ვექტორების პროექციათა სხვაობისა. ვექტორების სხვაობას. ვექტორების სხვაობის პროექცია მოცემულ ღერძზე ტოლია ამავე ღერძზე ვექტორების პროექციათა სხვაობისა.
| 






