16. გადააგილება, სიჩქარე და აჩქარება მრუდწირული მოძრაობისას

როგორც ვიცით, წრფივი მოძრაობისას სიჩქარისა და გადაადგილების ვექტორები ყოველთვის ერთი წრფის გასწვრივაა მიმართული. როგორია სიჩქარისა და გადაადგილების მიმართულება მრუდწირული  მოძრაობოისას? ამ კითხვაზე პასუხის გასაცემად ვისარგებლოთ  იმავე ხერხით, რომელიც გამოვიყენეთ მყისი სიჩქარის შესასწავლად.

გადაადგილება ქორდების გასწვრივ.

 51-ე სურათზე გამოსახულია რაღაც მრუდწირული ტრაექტორია. დავუშვათ, რომ მასზე A-დან B წერტილამდე მოძრაობს სხეული. სხეულის მიერ გავლილი გზა იქნება რკალი, ხოლო გადაადგილება- ვექტორი. რა თქმა უნდა,  მოძრაობისას სხეული სიჩქარის მიმართულება არ ემთხვევა გადაადგილების ვექტორის მიმართულებას (წინააღმდეგ შემთხვევაში, სხეული იმოძრავებდა AB წრფის გასწვრივ) A და B წერტილებს შორის გავავლოთ რამდენიმე ქორდა

(სურ. 52) და წარმოვიდგინოთ, რომ სხეული მოძრაობს ამ ქორდაზე. თითოულ მათგანზე სხეული წრფივად მოძრაობს და სიჩქარის ვექტორიც მიმართულია შესაბამისი ქორდის გასწვრივ.

მყისი სიჩქარე მიმართულია მხების გასწვრივ. ეს წრფივი უბნები (ქორდები) შევამციროთ (სურ. 53). თითოეულ ქორდაზე სიჩქარის ვექტორი კვლავ ქორდის გასწვრივ იქნება მიმართული. მაგრამ ვხედავთ, რომ ეს ტეხილი წირი ახლა უკვე მდოვრე მრუდს ჰგავს.

ცხადია თუ წრფივი უბნების შემცირებას განვაგრძობთ, ისისნი თითქმის წერტილებად იქცევა და ტეხილი წირი მდოვრე მრუდად გარდაიქმნება. სიჩქარე კი ამ მრუდის ნებისმიერ წერტილში მიმართული იქნება ამავე წერტილზე გავლებული მხების გასწვრივ (სურ. 54)

მრუდწირული ტრაექტორიის ნებისმიერ წერტილში სხეულის მოძრაობის სიჩქარე მიმართულია ამ წერტილზე გავლებული მხების გასწვრივ.

მრუდწირული მოძრაობისას სიჩქარე მართლაც მხების გასწვრივაამიმართული, დავრწმუნდებით, თუ დავაკვირდებით მაგალითად, სალესის მოძრაობას (სურ. 55). თუ სალესის მბრუნავ ქვას ფოლადის ღეროთი შევეხებით, ქვას ნაპერწკლები გასცვივდება. ეს ნაპერწკლები ქვას მომწყდარი გავარვარებული ნაპერწკლებია. ისინი იმავე სიჩქარით  მოძრაობენ, რომელიც ჰქონდათ ქვიდან მოწყვეტის მომენტში.კარგად ჩანს, რომ ნაპერწკლები მოძრაობენ წრეწირის იმ წერტილში გავლებული მხების გასწვრივ, სადაც ღერო ქვას ეხება. წრეწირის მხებს

ემთხვევა აგრეთვე მობუქსავე ავტომობილის თვლებს მომწყდარი შხეფების მოძრაობის მიმართულება (სურ. 56).

ამრიგად მრუდწირული ტრაექტორიის სხვადასხვა წერტილში სხეულის მყის სიჩქარეს სხვადასხვა მიმართულება აქვს (სურ. 57). სიჩქარის მოდული კი შეიძლება ყველგან ერთნაირი იყოს (სურ. 57), ანდა იცვლებოდეს წერტილიდან წერტილამდე (სურ. 58).

მაგრამ სიჩქარის მოდული უცვლელი რომ იყოს, სიჩქარე მაინც ვერ ჩაითვლება მუდმივად, ვინაიდან იგი ვექტორული სიდიდეა.

ვექტორული სიდიდეებისათვის კი მოდული და მიმართულება ერთნაირად მნიშვნელოვანია. ამის გამო მრუდწირული მოძრაობა ყოველთვის აჩქარებული მოძრაობაა (მაშინაც კი, როცა სიჩქარის მოდული არ იცვლება).

მრუდწირული მოძრაობისას შეიძლება იცვლებოდეს სიჩქარის მოდულიცა და მიმართულებაც. ჩვენ კი მხოლოდ ისეთ მრუდწირულ მოძრაობას განვიხილავთ, როცა სიჩქარის მოდული არ აცვლება. ასეთ მოძრაობას თანაბარმრუდწირულ მოძრაობას უწოდებენ. ამგვარი მოძრაობისას აჩქარება მხოლოდ სიჩქარის ვექტორის მიმართულების ცვლილებასთანაა დაკავშირებული. როგორ არის მიმართული აჩქარება და რას უდრის იგი?

მრუდწირული მოძრაობა წრეწირის რკალებზე მოძრაობაა. აჩქარების მოდულიცა და მიმართულებაც დამოკიდებული უნდა იყოს მრუდწირული ტრაექტორიის ფორმაზე. განსხვავებული ფორმის მრუდწირული ტრაექტორია უამრავია. მაგრამ ჩვენ არ მოგვიწევს თითოეული მათგანის განხილვა.

59-ე სურათზე გამოსახულია  სხეულის მოძრაობის რთული ტრაექტორია. სურათიდან ჩანს, რომ ამ ტრაექტორიის ცალკეული უბანი დაახლოებით იმ წრეწირების რკალებია, რომლებიც წყვეტილი წირებითაა გამოსახული. მაგალითად KL და BM უბნები მცირერადიუსიანი წრეწირის რკალებია. EF უბანი კი-დიდრადიუსიანი წრეწირისა.

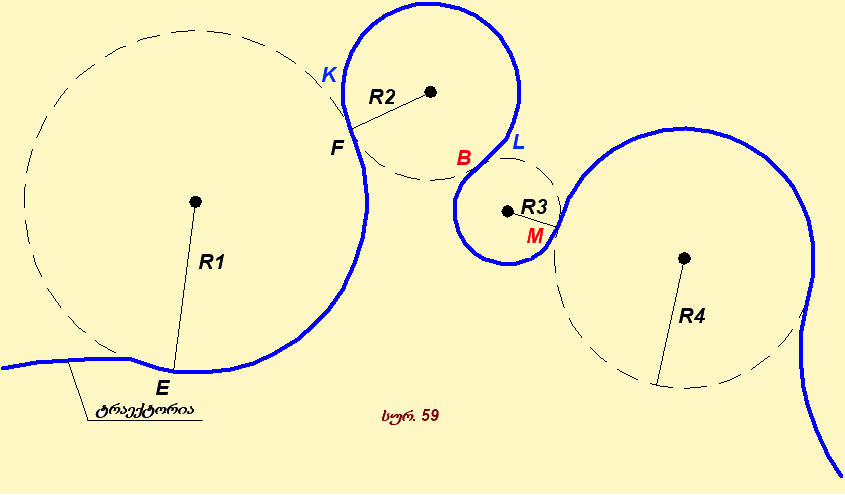
ამრიგად, ნებისმიერ მრუდწირულ ტრაექტორიაზე მოძრაობა მიახლოებით შეიძლება წარმოვადგინოთ როგორც მოძრაობა რომელიღაც წრეწირების რკალებზე. ამიტომ მრუდწირული თანაბარი მოძრაობის აჩქარების გასაგებად საკმარისია განვსაზღვროთ წრეწირზე თანაბარი მოძრაობის აჩქარება.